ВВЕДЕНИЕ

Анализ формальных понятий [Ganter, 1999], растущие пирамидальные сети [Гладун, 2004], терминологические сети [Мальковский и др., 2012] - вот далеко не полный перечень подходов к формированию понятийных структур. Несмотря на различия в постановках задач, в методах их решения, в получаемых результатах и в областях применения, вопрос о сравнении родственных подходов является вполне закономерным. В настоящей работе излагается взгляд на терминологические сети как на частично упорядоченные множества - результат анализа формальных понятий.
 

1. Терминологические сети

Терминологические сети представляют собой подкласс семантических сетей для определений терминов из одной или нескольких проблемных областей [Мальковский и др., 2012]. Построением терминологической сети занимается научный редактор, в помощь которому предоставлен разнообразный программный инструментарий. Деятельность редактора по построению терминологической сети является творческой, но весьма регламентированной, что позволяет (с определенными оговорками) говорить об объективном характере создаваемой им сети.

Вершинами терминологической сети являются словарные статьи, каждая из которых определяет некоторый термин, его синонимы, а также содержит иную "сопутствующую" информацию. Предполагается, что каждому термину сети соответствует некоторое понятие проблемной области. В данном случае понятие понимается вполне традиционно - как совокупность объектов (объем понятия), обладающих общими свойствами (содержание понятия), отличающих объекты понятия от прочих объектов.

Для терминологических сетей характерно использование ограниченного количества бинарных отношений, связывающих вершины. Так, в проекте "Универсальное терминологическое пространство" (УТП) между определениями 53'477 терминов установлены связи двух типов:
— отношение "это-есть" (34'566 экземпляров);
— отношение "относится-к" (41'003 экземпляра), включающее в себя все прочие типы бинарных отношений.

УТП изменяется во времени за счет вовлечения новой терминологии и корректировки ранее включенных терминов, их определений и связей. В дальнейшем нас будут интересовать связи только первого типа, посредством которых задаются родовидовые отношения между понятиями.

При построении УТП соотношения между понятиями-проблемной-области устанавливает редактор, присваивая некоторым вершинам УТП понятийный статус. С формальной точки зрения понятийная вершина отличается от обыкновенной тем, что обладает специально сконструированным уникальным именем и может служить входящей вершиной для ориентированных дуг бинарных отношений. Существует довольно обширный арсенал приемов, позволяющих редактору принять решение об учреждении новой понятийной вершины.

Часто информация о семантическом окружении [Гринев-Гриневич, 2009] понятия в явном виде содержится в определении термина, причем для родовидовых отношений в практике составления толковых словарей закрепились устойчивые шаблоны описаний. Так из следующего определения:

Таможенная пошлина - налог, взимаемый государством с провозимых через национальную границу товаров по ставкам, предусмотренным таможенным тарифом. По объекту обложения различают ввозимые, вывозимые и транзитные таможенные пошлины. По методу исчисления различают адвалорные, специфические и комбинированные таможенные пошлины.

немедленно вытекают

(А) факт существования понятия "Таможенные пошлины", наименование которого построено из определяемого термина переходом ко множественному числу и объем которого составляют всевозможные "налоги, взимаемые государством с провозимых через национальную границу товаров по ставкам, предусмотренным таможенным тарифом";

(Б) наличие родовидовой связи между понятиями "Таможенные пошлины" и "Налоги"; и

(В) существование шести подвидов понятия "Таможенные пошлины", порожденных двумя классификациями на элементах объема:
B.1.1 "Ввозимые таможенные пошлины",
B.1.2 "Ввозимые таможенные пошлины",
B.1.3 "Транзитивные таможенные пошлины",
B.2.1 "Адвалорные таможенные пошлины",
B.2.1 "Специфические таможенные пошлины" и
B.2.3 "Комбинированные таможенные пошлины".

В приведенном анализе конкретного определения существенно используются, во-первых, классификационный характер [Гринев-Гриневич, 2009] терминологической системы таможенного дела, а, во-вторых, неявно используется гипотеза о возможности выявления объективно существующих понятийных отношений из текстовых определений [Шелов, 2003].

При построении УТП реальные трудности возникают при работе с полиморфными [Шелов, 2003] определениями, допускающими неоднозначные толкования. В этом случае основным приемом структурирования выступает сопоставление определений, позволяющее путем логических выводов и поискам компромиссов выявить/установить связи между понятиями. По результатам сопоставления в УТП возникают общие понятийные вершины -суть- вершины, связанные родовидовыми отношениями с двумя или более понятийными вершинами более высокого уровня общности. Примеры общих понятий "Музыкальные комедии" и "Географические атласы" представлены на рисунках 5 и 6. Важно отметить, что наличие в УТП общих понятий выводит родовидовую структуру понятийных отношений из класса древовидных иерархий.

При работе с большим количеством понятий естественным образом возникает необходимость их объединения в тематические кластеры, каждый из которых соответствует некоторой проблемной области или отрасли науки. В существующей версии УТП представлены 183 тематических кластера, содержащие от 10 до 100 понятий. С точки зрения техники реализации каждый кластер представляет собой вершину УТП, с которой связаны понятийные вершины; для связи используется особый подвид отношений "относится-к". Отметим, что вершины терминологической сети, отвечающие кластерам, не входят в состав родовидовой структуры.
 

2. Анализ формальных понятий

Самый популярный подход к формированию понятийных структур связан с анализом формальных понятий (АФП). Каждое формальное понятие есть пара множеств

Объем // Содержание.

Предполагается, что Объем - это подмножество объектов из известного множества G, а Содержание - подмножество признаков из M, одновременно присущих исключительно объектам Объема. Подмножество К декартова произведения G × M, именуемое контекстом, однозначно порождает множество формальных понятий, на котором рассматривается естественное отношение порядка:

(G₁ // M₁) ⊆ (G₂ // M₂)  ⇔  G₁ ≤ G₂

Установлено [Ganter, 1999], что для заданного контекста K множество формальных понятий образует полную решетку [Биркгоф, 1984], по которой, в свою очередь, однозначно определяется диаграмма Хассе H(K) - см., например, рисунок 1.
 

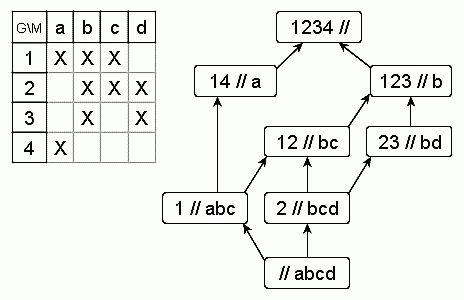Рисунок 1 - Контекст K1 и диаграмма Хассе H(K1)

Алгоритмы конструирования решеток по известному контексту известны [Кузнецов, 2004]. На рисунке 1 контекст K₁ задан в виде таблицы, строки которой соответствуют G = { 1, 2, 3, 4 }, а столбцы - M = { a, b, c, d }; элементы K₁ отмечены в таблице символом X. В общей сложности контекст K₁ позволяет построить восемь формальных понятий, причем два из них - "1234 //" и "// abcd" - фактически от контекста не зависят, они представляют собой "G // ∅" и "∅ // M" и играют роли наибольшего элемента I и наименьшего элемента O полной решетки формальных понятий.

Простейшие (в некотором смысле) диаграммы полных решеток, именуемые в дальнейшем модельными диаграммами, состоят
— из вершин O', p₁, ..., p_n, q₁, ..., q_m, I'; и
— из ориентированных ребер

(O', p₁), (p₁, p₂), ..., (p_n, I'),
(O', q₁), (q₁, q₂), ..., (q_m, I').

Конкретный вид модельной диаграммы - рисунок 2(а) и 2(б) - определяется парой чисел n ≥ 1 и m ≥ 1, которая записывается в виде формулы n+m. Считается, что
— вершине O отвечает наименьший элемент диаграммы;
— вершине I отвечает наибольший элемент;
— в каждом ориентированном ребре (a,b) вершина b сопоставлена более широкому понятию, чем вершина a.

Из формальных соображений будем также называть модельными диаграммами двухполюсные сети вида 0+m - рисунок 2(в).
 

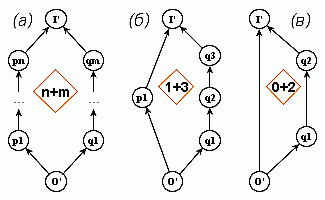Рисунок 2 - Модельные диаграммы

Сформулируем ряд структурно-топологических характеристик диаграмм Хассе, соответствующих полным решеткам.

Характеристика 1. В диаграмме Хассе полной решетки отсутствуют циклы.

Характеристика 2. В диаграмме Хассе полной решетки обязательно присутствуют наибольший и наименьший элементы I и O.

Характеристика 3. Диаграмма Хассе полной решетки не содержит подсети, изоморфные модельным диаграммам вида 0+m. Наличие таких подсетей эквивалентно существованию в диаграмме Хассе транзитивных ребер.

Характеристика 4. В диаграммах Хассе полных решеток допускаются специальные подсети, которые, во-первых, изоморфны модельным диаграммам вида n+m, где n ≥ 1 и m ≥ 1, и, во-вторых, не содержат элементов I и O. На рисунке 3(а) приводится специальная подсеть вида 1+1 для диаграммы Хассе H(K₁).

Соответствие двухполюсной сети характеристикам 1-3 позволяет говорить о ее "похожести" на некоторую диаграмму полной решетки. Наличие же в двухполюсной сети специальных подсетей позволяет судить о ее "нетривиальности" как решетки.
 

3. Классификация понятий

Диаграмма Хассе является двухполюсной сетью без циклов; обратное утверждение неверно. Будем рассматривать внутренние вершины двухполюсных сетей без циклов. Исключая из рассмотрения полюсы, которым зачастую невозможно сопоставить понятия проблемной области, определим три подкласса внутренних вершин. Внутреннюю вершину будем называть
— общей, если из нее исходят два или более ребер;
— узловой, если в нее заходят два или более ребер;
— простой, если в нее заходит ровно одно ребро, исходящее из некоторой другой внутренней вершины.

На рисунке 3(б) приводятся типы вершин для диаграммы Хассе H(K1).
 

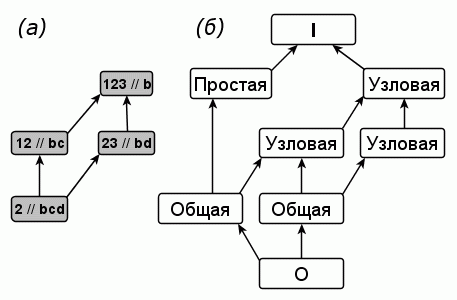Рисунок 3 - Типы вершин в двухполюсных сетях

Замечание 1. В конкретных диаграммах Хассе могут существовать (а) вершины, не соответствующие ни одному приведенному классу вершин, (б) узловые общие вершины и (в) узловые простые вершины. Например, в диаграмме H(K₄) - рисунок 4 - вершина "3 // bde" не относится ни к одному из трех классов.

Замечание 2. Наличие в диаграммах Хассе общих вершин, позволяет моделировать иерархические но не обязательно древовидные структуры понятий.

Замечание 3. В полных решетках простым вершинам соответствует элементы решеток неразложимые в объединение [Гуров, 2004].

Замечание 4. В развивающихся понятийных структурах простые вершины способны превращаться в узловые. Так, на рисунке 4 приведен контекст K₄, который отличается от контекста K₁ наличием только одного нового признака e для объекта 3, однако в диаграмме H(K₄) бывшая простая вершина "23 // bd" стала узловой.
 

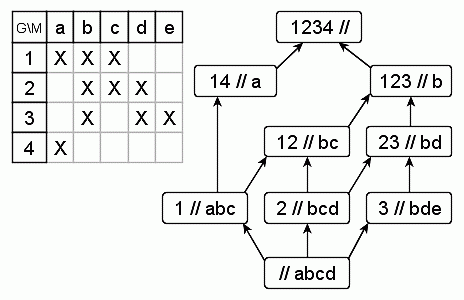Рисунок 4 - Контекст K4 и диаграмма Хассе H(K4)

Замечание 5. В растущих пирамидальных сетях [Гладун, 2004], предназначенных для порождения и представления понятийных структур, простые вершины вообще не допускаются.
 

4. УТП как объект исследования

(УТП ⇒ УТП*) Каждая версия УТП содержит некоторое количество частично описанных понятий, присутствующих в терминологической сети, но не раскрытых посредством перечисления подвидов и отношений с другими понятиями. С одной стороны, такого рода "полупонятия" в УТП неизбежны, а с другой стороны, они способно серьезно повлиять на количественные показатели понятийной структуры. В связи с этим для исследования были отобраны только понятийные вершины УТП и родовидовые связи между ними. Усеченная таким образом часть УТП - обозначим ее УТП* - насчитывает 9'043 (из 53'477) вершин-понятий и 7'009 связей между ними.

(УТП* ⇒ УТП**) Из соотношения вершин и ребер следует, что УТП* не является связным графом. Как показывают расчеты, в составе УТП* насчитываются 1999 компонент, состоящих из изолированных понятий-вершин, и 261 компонента, каждая из которых состоит из двух вершин. Эти 2260 компонент также следует исключить из анализа по мотивам недостаточности описания. Таким образом, в окончательном варианте графа - обозначим его УТП** - имеется 5'522 вершин и 6'748 связей между ними.

Ориентированный граф УТП** состоит из 316 компонент связности, порождающих разбиение множества вершин УТП** на 316 подмножеств. Подавляющая часть - 4'483 из 5'522 (81%) вершин УТП** входят в одну самую крупную компоненту. Вторая по размеру компонента имеет 86 вершин, третья - 54.
 

5. Свойства УТП** как решетки

Обработка УТП** позволяет сформулировать ряд согласованных выводов о свойствах родовидовых связей терминологических сетей.

Первое. Как правило, в родовидовой структуре УТП циклы отсутствуют. Оговорка "как правило" здесь и далее означает, что обнаруженные в УТП дефекты представляют собой подлежащие устранению ошибки редактирования.

Второе. В ориентированном графе УТП** имеется 3'783 вершин без заходящих ребер и 617 вершин без исходящих ребер. Разнообразие связанных с этим вершинами понятий чрезвычайно широко: от "CGI-приложений" до "Уроков классического танца" и от "Денежных систем" до "Тушения пожаров". Отсюда следует, что для УТП невозможно определить термины для наибольшего и наименьшего элементов, то есть элементы I и O могут существовать в УТП** только как абстрактные вершины, не связанные с определенными терминами. Вместе с тем, явно избыточное количество понятий верхнего уровня со всей очевидностью ставит вопрос о терминологическом представлении в УТП "нерасчлененного смыслового континуума" [Морковкин, 1970].

Третье. Как правило, в ориентированном графе УТП** не содержатся модельные диаграммы вида 0+m. Тем не менее отдельные диаграммы вида 0+3 и 0+4 вносятся в УТП вполне сознательно.

Четвертое. Ориентированный граф УТП** содержит 295 модельных диаграмм, из которых:
145 диаграмм    (49%)    вида 1+1;
  88 диаграмм    (30%)    вида 1+2;
  17 диаграмм    (  6%)    вида 2+2;
  15 диаграмм    (  5%)    вида 1+3;
  13 диаграмм    (  4%)    вида 2+3.
В большинстве случаев выявленные диаграммы не выводят за пределы тематических кластеров. На рисунке 5 представлена типичная диаграмма, связывающая четыре понятия из тематического кластера "Театральное искусство".
 

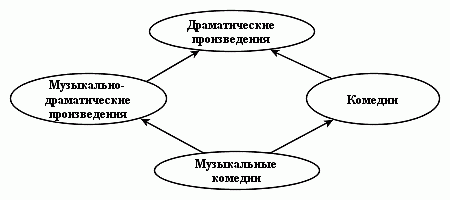Рисунок 5 - Диаграмма для кластера "Театральное искусство"

В некоторых случаях в одну модельную диаграмму попадают понятия из родственных кластеров:

"Горные породы" -и- "Полезные ископаемые",
 "Ценные бумаги" -и- "Деньги",
  "Судовождение" -и- "Суда".

Фактически выявление в УТП модельных диаграмм оказывается достаточно продуктивной эвристикой для алгоритма автоматической кластеризации понятий по родовидовым связям.

Незначительно количество модельных диаграмм позволяет выявить в УТП нетривиальные связи между понятиями. Пример такой диаграммы приводится на рисунке 6. Восемь понятий этой диаграммы принадлежат тематическим кластерам "Документы", "Издания", "Информация" и "Географические карты".
 

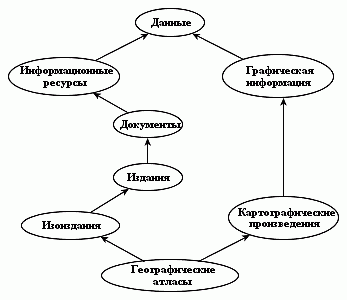Рисунок 6 - Модельная диаграмма 2+4

Модельные диаграммы, обнаруженные в УТП**, имеют общие вершины и ребра, что позволяет рассматривать модельные подграфы -суть- максимальные подграфы УТП**, целиком составленные из двух и более модельных диаграмм. По определению модельные подграфы не имеют общих вершин и ребер.

Пятое. В ориентированном графе УТП** обнаружены 43 модельных подграфа, самый крупный из которых имеет 128 вершин-понятий и 173 ребра, а самый мелкий - 6 вершин и 7 ребер. Семнадцать модельных подграфов (40%) решетками не являются, причем с увеличением размеров модельных подграфов вероятность "выпадения" из класса решеток возрастает, а все модельные подграфы, содержащие более 15 вершин и 20 ребер, гарантированно не являются решетками. При проверке свойств модельных графов допускалось отсутствие в решетках наибольшего и/или наименьшего элементов, предполагалось, что универсальные грани I и O можно достроить. На рисунке 7 представлена структура одного из модельных подграфов, который не является решеткой - у него нем отсутствуют inf {7, 11}, sup {1, 6} и др.

Шестое. В ориентированном графе УТП** имеется 783 общие понятийные вершины, 374 из которых являются наименьшими элементам модельных диаграмм. Таким образом, в УТП** для 409 общих вершин не нашлось явно сформулированных понятий, способных сыграть роль наибольших элементов соответствующих модельных диаграмм.

(409 / 783) * 100% = 52%.

Седьмое. В ориентированном графе УТП** выявленные модельные диаграммы покрывают 1319 ребер из 6'748. Остальные 5'429 ребер не входят в диаграммы. Доля "неохваченных" ребер составляет

(5429 / 6748) * 100% = 80%.

Восьмое. В ориентированном графе УТП** выявленные модельные диаграммы покрывают 1'048 вершин из 5'522. Остальные 4'474 вершин не входят в диаграммы. Доля "неохваченных" вершин составляет

(4474 / 5522) * 100% = 81%.

Девятое. В ориентированном графе УТП** имеется 191 простая вершина, что составляет 3.5% от общего количества вершин. Как показывают дополнительные исследования незначительная доля простых вершин характерна для всех версий УТП.
 

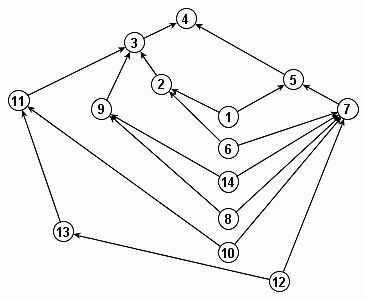Рисунок 7 - Модельный подграф

В совокупности девять приведенных свойств образуют своеобразную систему косвенных свидетельств о наличии и характере связей между решеточно упорядоченными множествами и терминологическими сетями.

Анализ УТП на наличие модельных диаграмм с последующим построением и исследованием модельных подграфов
— позволяет обнаруживать некоторые дефекты УТП (свойства 1 и 3);
— предлагает подход к автоматической кластеризации понятий (свойство 4);
— открывает возможность data mining [Багсегян и др., 2004] в терминологических сетях (свойство 4).
 

Заключение

По результатам проведенных исследований соотношение между двумя методологиями конструирования родовидовых связей понятийных структур представляется достаточно сложным. С одной стороны, слишком большое количество реально существующих отношений между понятиями не сводятся к полным решеткам. С другой стороны, полные решетки понятий вполне естественны для хорошо структурированных или отдельно взятых терминологических систем. Соотношения такого рода характерны для взаимодополняющих методик.
 

Библиографический список

[Барсегян и др., 2004] Методы и модели анализа данных: OLAP и Data Mining / А.А.Барсегян, М.С.Куприянов, В.В Степаненко, И.И.Холод - СПб.: БХВ-Петербург, 2004.

[Биркгоф, 1984] Теория решеток / Г. Биркгоф - М.: Наука, 1984.

[Гладун, 2004] Гладун В.П. Растущие пирамидальные сети сети / В.П.Гладун // Новости искусственного интеллекта. - 2004, № 1. С.30-40.

[Гринев-Гриневич, 2009] Введение в терминографию: Как просто и легко составить словарь / С.В.Гринев-Гриневич - М.: ЛИБРОКОМ, 2009.

[Гринев-Гриневич, 2008] Терминоведение / С.В.Гринев-Гриневич - М.: Академия, 2008.

[Гуров, 2004] Упорядоченные множества и универсальная алгебра. Вводный курс / С.И.Гуров - М.: ВМК МГУ, 2004.

[Мальковский и др., 2012] Мальковский М.Г., Терминологические сети / M.Г.Мальковский, С.Ю.Соловьев // OSTIS-2012. Материалы конференции. С. 77-82
www.park.glossary.ru/serios/theory10.php

[Морковкин, 1970] Морковкин, В.В. Идеографические словари / В.В.Морковкин - М.: Изд-во Моск.ун-та, 1970. - 72 c.

[Кузнецов, 2004] Кузнецов С.О. Методы теории решеток и анализа формальных понятий в машинном обучении / С.О. Кузнецов // Новости искусственного интеллекта. - 2004, № 3. С.19-31.

[Шелов, 2003] Термин. Терминологичность. Терминологические определения / С.Д.Шелов - СПб.: Филологический факультет СПбГУ, 2003.

[Ganter, 1999] Formal Concept Analysis: Mathematical Foundations / B.Ganter, G.Stumme, R.Wille - Berlin: Springer, 1999.

--------- * ---------

Точная ссылка: Мальковский М.Г., Соловьев С.Ю.
Исследование родовидовых отношений в терминологических сетях.
// Материалы III Международной научно-технической конференции
"Открытые семантические технологии проектирования интеллектуальных систем (OSTIS-2013)"
- Минск: БГУИР, 2013. С.147-152

Copyright ©
2000-2022
Web-and-Press