|
н а п р а в а х р е к л а м ы
|
|

|
Чтение:
1
| 2
| 3
| 4
| 5
| 6
| 7
| 8
| 9
| 10
| 11
| 12
| 13
| 14
| 15
| 16
| 17
| 18
|
С.Ю.Соловьев
Эквивалентные преобразования
контекстно-свободных грамматик
|
Серьезное
чтение
на glossary.ru
точная ссылка
|
Введение
В теории формальных языков известно большое количество эквивалентных
преобразований контекстно-свободных грамматик (КС-грамматик). Помимо
прочего это означает, что один и тот же КС-язык может порождаться весьма
непохожими грамматиками. В настоящей работе эквивалентные преобразования
грамматик рассматриваются с точки зрения удаления конструкций
"несущественных" для порождаемого языка.
Контекстно-свободной грамматикой [1] называется четверка
G = < N, ∑, P, S >, где
| N – алфавит нетерминальных символов (нетерминалов); |
| ∑ – непересекающийся с N алфавит |
| терминальных символов (терминалов); |
| P – конечное множество правил вывода вида A → α, |
| где A ∈ N, α - цепочка символов из N ∪ ∑; |
| S – выделенный символ из N, именуемый начальным символом. |
В последующих выкладках будем полагать, что действуют следующие соглашения:
- A, B, C обозначают нетерминалы; S - начальный символ;
- a, b, c, d — терминальные символы;
- α, β, γ, σ — цепочки символов из N ∪ ∑
- x, y, z — цепочки символов (предложения) из ∑ ;
- e — пустая цепочка нулевой длины;
- запись A → α1 | ... | αn,
означает множество правил
{ A → α1 , ..., A → αn };
- запись α ⇒G β означает, что
α = α1Aα2 ,
β = α1γα2 и
A → γ ∈ P; в этом случае будем говорить, что
цепочка β непосредственно выводима из цепочки α в грамматике G;
- L(G) = { x | S ⇒*G x }
— язык, порождаемый грамматикой G.
Принятые соглашения позволяют, в частности, задавать
КС-грамматики простым перечислением правил вывода.
КС#грамматики
Каждая контекстно-свободная грамматика G = < N, ∑, P, S >
порождает семейство грамматик G(A) = < N, ∑, P, A >, где A ∈ N.
Для начального символа S имеем: G(S) = G и L(G(S)) = L(G) .
В общем случае КС-язык L(G(A))
есть реализация нетерминала A в классе терминальных цепочек.
В дальнейшем изложении будем рассматривать только
такие КС-грамматики < N, ∑, P, S >, в которых:
- отсутствуют правила с пустой правой частью; и
- имеется правило S → #,
причем терминальный символ # в других правилах не встречается.
Для КС-грамматик, удовлетворяющих перечисленным свойствам, будем
использовать обозначение КС#грамматики.
С точки зрения порождаемых языков приведенные ограничения не являются
существенными. Любой КС-язык L может быть получен из КС#языка L#
одним из двух способов:
либо L = L# \ { # } ,
либо L = (L# \ { # }) ∪ { e };
соответствующая КС-грамматика получается
либо посредством удаления правила S → #,
либо посредством его замены на правило S → e.
Вместе с тем, использование дополнительного символа # позволяет
естественным образом вывести начальный символ S из-под действия многих
эквивалентных преобразований.
Остановимся на одном из преобразований КС-грамматик, связанным с изменением
языков L(G(A)), A ≠ S. В качестве неформально введения в задачу
рассмотрим цепочки abcg, abcfg и abdсdg. Эти цепочки имеют общий префикс ab
и общий суффикс g. В более изощренных случаях необходимо точно оговорить,
что считать общим префиксом и/или суффиксом:
- для { a, ab, abb } префикс и суффикс отсутствуют;
- для { abc, abcc, abccс } префикс = ab, суффикс отсутствует;
- для { abc, abbc, abbbс } префикс = ab, суффикс отсутствует и пр.
В общем случае, после удаления общих префикса и суффикса не должна
возникать пустая цепочка. Кроме того, будем исходить из того, что сначала
определяется префикс, а затем — суффикс.
|
Если язык L(G(A)) имеет непустой общий префикс x,
| |
то будем говорить, что нетерминал A имеет префикс x.
| |
Если язык L(G(A)) имеет непустой общий суффикс z,
| |
то будем говорить, что нетерминал A имеет суффикс z.
|
Продолжая неформальное введение, рассмотрим КС-грамматику
G: S → A+A | gb
A → abcg | abcfg | abdсdg
Здесь язык L(G(A)) = { abcg, abcfg, abdcdg } задан в явном виде.
У нетерминала A префикс ab и суффикс g можно изъять и передать "вышестоящему"
нетерминалу S , при этом грамматика примет следующий вид
G': S → abA'g+abA'g | gb
A' → c | cf | dсd
В грамматике G' нетерминал A' не имеет ни префикса ни суффикса.
Понятно, что грамматики G и G' эквивалентны. Возникает вопрос
о возможности изъятия префиксов и суффиксов нетермналов
для КС-грамматик общего вида. Отметим, что в данном случае
изъятие рассматривается как эквивалентное преобразование грамматик.
Нетерминалы, у которых можно забирать префиксы и суффиксы,
удовлетворяют естественным условиям:
| L(G(A)) = конкатенация(a,L) |
|
(L) |
|
и/или L(G(A)) = конкатенация(L,a) |
|
(R) |
| где L - некоторый язык, e ∉ L. |
|
|
Однако приведенные условия являются слишком общими; можно показать
алгоритмическую неразрешимость задачи изъятия префиксов и суффиксов у всех
нетерминалов, удовлетворяющих условиям (L) и (R). Пойдем по пути уточнения
класса нетерминалов, у которых можно "безнаказанно" забирать префиксы и
суффиксы.
LD-преобразование КС#грамматик
Подмножество нетерминалов КС#грамматики G = < N, ∑, P, S >
будем называть делимым-слева относительно терминала a, и
будем будем его обозначать LD(a),
если множество правил вывода P образуют правила трех типов:
тип 1: A → aα, где A ∈ LD(a) и α ≠ e;
тип 2: A → A0α, где A ∈ LD(a) и A0 ∈ LD(a)
тип 3: B → α, где B ∉ LD(a).
Понятно, что
если A ∈ LD(a), то L(G(A)) обязательно удовлетворяет условию (L);
если B ∉ LD(a), то L(G(B)) может удовлетворять или не удовлетворять условию (L) .
Например:
GT: S → A+A | Bg
A → ab | Aa
B → Dd | abd
D → a | aD
∀ x ∈ { a, b, d, g, + } D ∉ LD(x),
и, следовательно, B ∉ LD(x).
LD(a) = { A },
правила типа 1: A → ab;
правила типа 2: A → Aa;
правила типа 3: S → A+A, S → Bg, B → Dd,
B → abd,
D → а,
D → аD.
A ∈ LD(a);
L(GT(A)) = { aban | n ≥ 0 } =
{ ax | x = ban, n ≥ 0 }.
B ∉ LD(a);
L(GT(B)) = { and | n ≥ 1 }
∪ { abd } =
{ ax | x = and / bd, n ≥ 2 }.
Предложения из L(GT(D)) не сводимы к виду ax, где x ≠ e.
Конец примера.
Каждому делимому-слева подмножеству нетерминалов
LD(a) = { A1, A2, ... }
поставим во взаимнооднозначное соответствие подмножество
ранее не использовавшихся нетерминальных символов
LD'(a) = { A'1, A'2, ... }.
Если в контексте некоторой КС-грамматики известно множество LD(a),
то можно рассматривать преобразование цепочек W, заключающееся в выполнении
всевозможных подстановок
aA'i вместо Ai.
Цепочка W(α) получается
из цепочки α посредством замены всех символов A из LD(a) на цепочки
из двух символов aА', где А' ∈ LD'(a). Обратное преобразование W -1
заменяет в заданной цепочке все вхождения aA'i на соответствующие
нетерминалы Ai. Обратное преобразование полностью удаляет из заданной
цепочки α все символы LD'(a) только в том случае,
когда непосредственно перед символом из LD'(a) располагается символ a.
Например, в грамматике GT
для LD(a) = { A } имеем:
W(Aa+A+aBg) = &aA'a+aA'+aBg,
W-1(&aA'a+bA'+aBg) = Aa+bA'+aBg,
W-1(&aA'a+aA') = Aa+A
Пусть LD(a) - подмножество делимых-слева нетерминалов некоторой
КС#грамматики G = < N, ∑, P, S >, определим грамматику
GW = < NW, ∑, PW, S >
следующим образом:
NW = (LD'(a) ∪ N) \ LD(a), а
PW построено так:
- если A → aα есть правило типа 1 грамматики G, то A' → W(α) ∈ PW;
- если A → A0α есть правило типа 2 грамматики G, то A' → A'0W(α) ∈ PW;
- если B → α есть правило типа 3 грамматики G, то B → W(α) ∈ PW.
Например, для множества LD(a) = { A } грамматики
G: S → A | A+A | #
A → ab | A+A | A-A
имеем:
GW: S → aA' | aA'+aA' | #
A' → b | A'+aA' | A'-aA'
Заметим, что преобразование грамматики G в грамматику GW
(LD-преобразование) возможно только в том случае, когда в G найдется хотя бы
одно непустое множество нетерминалов LD(a), более того, LD(a) является
существенным аргументом LD-преобразования.
Утверждение 1. L(G) ⊆ L(GW)
для КС#грамматики G = < N, ∑, P, S >.
Доказательство. Рассмотрим произвольное предложение x из L(G) и
некоторый левый вывод x в грамматике G.
S = σ0 ⇒G σ1 ⇒G ... ⇒G σk-1 ⇒G σk = x.
Докажем по индукции, что последовательность цепочек
W(σ0), ..., W(σk)
есть левый вывод предложения x в грамматике GW.
Из-за наличия правила S → # основной символ S не может входить ни в
одно множество делимых-слева нетерминалов. Поэтому
W(σ0) = W(S) = S,
то есть W(σ0) - цепочка, выводимая в GW.
Предположим, что для некоторого i, i < k, установлено, что
S = W(σ0) ⇒GW
W(σ1) ⇒GW ...
⇒GW
W(σi)
Покажем, что в этом случае W(σi) ⇒GW
W(σi+1).
Рассмотрим i+1-й этап левого вывода предложения x в грамматике G:
σi ⇒G σi+1.
По определению левого вывода:
σi = zCγ ⇒G zβγ = σi+1
причем C → β есть правило грамматики G.
Из-за наличия в грамматике G множества делимых-слева нетерминалов LD(a)
правило C → β может быть:
- либо типа 1: A → aα и тогда
| W(σi) |
= W(zAγ) |
= zaA'W(γ), |
| W(σi+1) |
= W(zaαγ) |
= zaW(α)W(γ), |
| |
то есть zaA'W(γ ) ⇒GW zaW(α)W(γ)
посредством правила A' → W(α) из PW;
|
- либо типа 2: A → A0α и тогда
| W(σi) |
= W(zAγ) |
= zaA'W(γ), |
| W(σi+1) |
= W(zA0αγ) |
= zaA'0W(α)W(γ), |
| |
то есть zaA'W(γ) ⇒GW zaA'0W(α)W(γ)
посредством правила A' → A'0W(α) из PW;
|
- либо типа 3: B → α и тогда
| W(σi) |
= W(zBγ) |
= zBW(γ), |
| W(σi+1) |
= W(zαγ) |
= zW(α)W(γ), |
| |
то есть zBW(γ) ⇒GW zW(α)W(γ)
посредством правила B → W(α) из PW;
|
Во всех трех случаях W(σi) ⇒GW W(σi+1)
и, следовательно, предложение x = W(σk)
выводимо в грамматике GW,
а значит L(G) ⊆ L(GW) .
Утверждение 1 доказано.
Утверждение 2. L(G) ⊇ L(GW) для КС#грамматики G.
Доказательство проведем индукцией по длине левого вывода некоторого
произвольного предложения x из L(GW).
S = σ0 ⇒GW
σ1 ⇒GW ...
⇒GW
σk-1 ⇒GW
σk = x
Покажем, что:
1и) в цепочках
σ0,
σ1, ...
σk-1,
σk
перед каждым символом из N'A размещается символ a; и
2и) последовательность цепочек
W-1(σ0),
W-1(σ1), ...
W-1(σk-1),
W-1(σk)
есть левый вывод предложения x.
Цепочка W-1(σ0) состоит из единственного
символа S и поэтому она удовлетворяет условиям 1и) и 2и).
Предположим, что для некоторого i, i < k, установлено, что:
1п) в цепочках
σ0,
σ1, ... ,
σi
перед каждым символом из N'A размещается символ a; и
2п) последовательность цепочек
S = W-1(σ0) ⇒G
W-1(σ1) ⇒G ... ,
⇒G
W-1(σi)
есть левый вывод предложения W-1(σi).
Рассмотрим переход σi ⇒GW σi+1
в левом выводе предложения x.
По определению левого вывода σi = zCγ, σi+1 = zβγ
и C → β
есть правило грамматики GW .
Отметим два обстоятельства.
Во-первых, в цепочке γ перед каждым символом из N'(a)
размещается символ a. Это следует из того, что
— в zCγ по индуктивному предположению 1п) перед
каждым символом из N'A размещается символ a; и
— в zCγ цепочка γ располагается непосредственно
за нетерминальным символом C и поэтому не может начинаться символом
из N'(a).
Во-вторых, по построению грамматики GW
правило C → β может быть
- либо A' → α, если оно получено из правила первого типа
A → aW-1(α) из G, и тогда
σi = zCγ = zA'γ = yaA'γ
на основании индуктивного предположения 1п),
| W-1(σi) |
= W-1(yaA'γ) |
= W-1(y)W-1(aA')W-1(γ) |
= yAW-1(γ), |
| W-1(σi+1) |
= W-1(yaαγ) |
= W-1(y)W-1(aα)W-1(γ) |
= yaW-1(α)W-1(γ), |
| |
то есть yAW-1(γ) ⇒G yaW-1(α)W-1(γ)
посредством правила A → aW-1(α);
|
- либо A' → A'0α, если оно получено из правила
второго типа A → A0W-1(α)
из G, и тогда
σi = zCγ = zA'γ = yaA'γ
на основании индуктивного предположения 1п),
| W-1(σi) |
= W-1(yaA'γ) |
= W-1(y)W-1(aA')W-1(γ) |
= yAW-1(γ), |
| W-1(σi+1) |
= W-1(yaA'0αγ) |
= W-1(y)W-1(aA'0α)W-1(γ) |
= yA0W-1(α)W-1(γ), |
| |
то есть yAW-1(γ) ⇒G yA0W-1(α)W-1(γ)
посредством правила A → A0W-1(α);
|
- либо B → α, если оно получено из правила третьего типа
B → W-1(α) из G,
и тогда σi = zCγ = zBγ,
| W-1(σi) |
= W-1(yBγ) |
= W-1(y)W-1(B)W-1(γ) |
= yBW-1(γ), |
| W-1(σi+1) |
= W-1(yαγ) |
= W-1(y)W-1(α)W-1(γ) |
= yW-1(α)W-1(γ), |
| |
то есть yBW-1(γ) ⇒G yW-1(α)W-1(γ)
посредством правила B → W-1(α).
|
Во всех трех случаях W(σi) ⇒G W(σi+1)
и, следовательно, предложение x = W(σk)
выводимо в грамматике G,
а значит L(G) ⊇ L(GW).
Утверждение 2 доказано.
Окончательно имеем следующее
Утверждение 3. L(G) = L(GW) для КС#грамматики G.
Другими словами, LD-преобразование грамматик является эквивалентным преобразованием.
Если КС#грамматика G одновременно является LL(1)-грамматикой [1], то в
LD-множества могут попасть только простые1 нетерминалы. Отсюда
следует, что LD-преобразование сохраняет класс LL(1)-грамматик.
|
|
1 Простым называется нетерминал A, для которого в грамматике имеется ровно одно правило A → α (A-правило).
|
|
RD-преобразование КС#грамматик
Аналогично LD-преобразованию вводится RD-преобразование КС#грамматик,
основанное на множестве RD-нетерминалов делимых-справа.
Подмножество нетерминалов КС#грамматики G = < N, ∑, P, S >
будем называть делимым-справа относительно терминала a, и
будем его обозначать RD(a),
если множество правил вывода P образуют правила трех типов:
| тип 1': |
A → αa, |
где A ∈ RD(a) и α ≠ e; |
| тип 2': |
A → αA0, |
где A ∈ RD(a) и A0 ∈ RD(a); |
| тип 3': |
B → α, |
где B ∉ RD(a). |
Если в КС-грамматике зафиксировано некоторое подмножество делимых-справа
нетерминалов RD(a), то в такой грамматике можно рассматривать преобразование
цепочек V. Цепочка V(α) получается из цепочки α посредством
замены всех символов A из RD(a) на цепочки из двух символов A'a, где
A' ∈ RD'(a).
Пусть RD(a) - подмножество делимых-справа нетерминальных символов
КС#грамматики G = < N, ∑, P, S >, определим
грамматику GV = < NV, ∑, PV, S >
следующим образом:
NV = ( RD'(a) ∪ N ) \ RD(a), а
PV построено так:
| если A → αa |
есть правило типа 1' грамматики G, то A' → V(α) |
∈ PV; |
| если A → αA0 |
есть правило типа 2' грамматики G, то A' → V(α)A'0 |
∈ PV; |
| если B → α |
есть правило типа 3' грамматики G, то B → V(α) |
∈ PV. |
Можно показать, что L(G) = L(GV), то есть RD-преобразование
КС#грамматики G в КС#грамматику GV относительно некоторого
непустого множества RD-нетерминалов является эквивалентным преобразованием.
Реализация эквивалентных преобразований КС-грамматик
Разнообразие преобразований КС-грамматик, а также необходимость их
многократного повторения порождает задачу совместного использования
эквивалентных преобразований. Как организовать процесс трансформации
заданной грамматики с тем, чтобы результирующая грамматика уже не
допускала ни одного заданного преобразования? Сложность состоит в том,
что одно преобразование может удалять из грамматики A-конструкции и
пополнять грамматику Б-конструкциями, а другое преобразование может
поступать ровно наоборот.
Прежде всего, отметим, что с алгоритмической точки зрения
каждое преобразование можно представить в следующем виде:
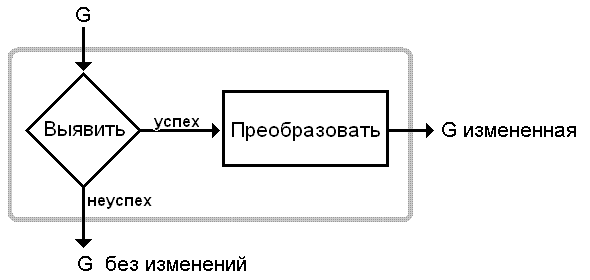
Например, в LD-преобразовании
этап "Выявить" состоит в нахождении некоторого непустого множества LD(a);
этап "Преобразовать" состоит в построении грамматики GW относительно найденного множества LD(a).
Фактически по успешной ветке может передаваться
некоторая информация, существенная для преобразования.
Не вдаваясь в подробности этапов, будем изображать
преобразование в виде прямоугольника со сглаженными углами.
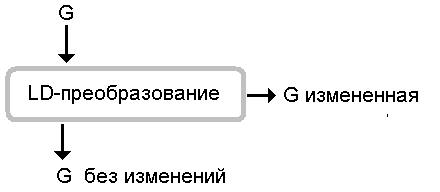
В этот прямоугольник
- сверху входит стрелка, соответствующая исходной грамматике;
- направо выходит стрелка, соответствующая измененной грамматике; и
- вниз выходит стрелка, соответствующая исходной грамматике, оставшейся без изменений.
С использованием принятых обозначений универсальная
схема управления преобразованиями грамматик выглядит так:
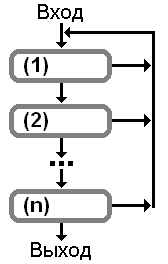
Нетрудно видеть, что универсальная схема
- полностью определяется последовательностью эквивалентных преобразований;
- имеет определенные достоинства; и
- порождает некоторые проблемы.
Достоинства. Универсальная схема гарантирует, что в результирующей
грамматике более нельзя выполнить ни одного эквивалентного преобразования
(1), (2), ..., (n).
Проблемы. Для каждого набора преобразований необходимо доказывать
корректность универсальной схемы, то есть необходимо доказывать конечность
последовательности преобразований. В отдельных, но важных случаях на
доказательстве корректности можно "сэкономить". В этих случаях конечность
процесса эквивалентных преобразований основывается на том, что каждое
преобразование уменьшает численную характеристику h исходной грамматики [2].
По определению величина h КС-грамматики G = < N, ∑, P, S > есть
| h(G) = |
∑ |
min { длина(x) | x ∈ L(G(A)) } |
|
A ∈ N |
|
Например, для рассмотренной ранее грамматики GT имеем:
min { длина (x) | x ∈ L(GT(D)) } = 1;
min { длина (x) | x ∈ L(GT(B)) } = 2;
min { длина (x) | x ∈ L(GT(A)) } = 2;
min { длина (x) | x ∈ L(GT(S)) } = 3;
и окончательно имеем: h(GT) = 1 + 2 + 2 + 3 = 8 .
Зачастую по результатам эквивалентного преобразования
1. одна часть нетерминалов сохраняет свои реализации неизменными, в том числе, начальный символ S, а
2. другая (непустая) часть нетерминалов:
2.1 либо вообще ликвидируется,
2.2 либо изменяет свою реализацию c L(G(A)) на L, где
| L = { y | xy ∈ L(G(A) } или |
| L = { y | yz ∈ L(G(A) } для некоторых непустых x и z. |
Преобразование, удовлетворяющее свойствам 1+2, уменьшает величину h.
Факт уменьшения величины h будем обозначать h-.
Например, LD-преобразование КС#грамматик относительно некоторого LD(a)
подпадает под случай 1+2.2 при x = a, z = e. Здесь первую часть нетерминалов
составляют N \ LD(a), а вторую - LD(a). Нетрудно показать, что
h(G) = h(GW) - R, где R - количество нетерминалов в LD(a).
Рассмотрим подвид универсальных схем эквивалентных
преобразований, представленный на следующем рисунке:
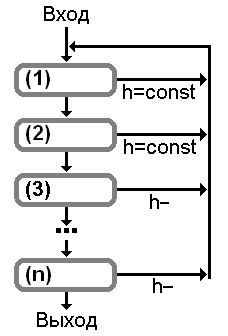
Здесь:
- преобразование (1) - необязательное устранение
бесполезных2 символов, в том числе:
- нетерминалов, которые не могут порождать терминальные цепочки; и
- правил вывода, содержащих недостижимые символы;
- преобразование (2) - необязательное устранение цепных3 правил;
- преобразования (3)..(n) - такие преобразования, которые уменьшают характеристику h.
|
|
2 Бесполезным [1] в грамматике G = < N, ∑, P, S > называется символ X ∈ N ∪ ∑, для которого в грамматике нет вывода вида S ⇒*G yXz ⇒*G yxz.
3 Цепным [1] называется правило вывода вида A → B.
|
|
Преобразования (1) и (2) давно и хорошо изучены, в общем случае они не
изменяют характеристику грамматики h, однако их использование совместно или
порознь не способно привести к зацикливанию. Что касается остальных
преобразований, то их выполнение порождает монотонно убывающую
последовательность положительных чисел
h1, h2, h3, ... .
Такая последовательность не может быть бесконечной, а значит корректность
подвида универсальных схем эквивалентных преобразований установлена.
К преобразованиям (3)..(n), в частности, относятся:
| устранение простых нетерминалов | - случай 1+2.1 (h-); |
| устранение нерекурсивных4 нетерминалов | - случай 1+2.1 (h-); |
| устранение избыточных нетерминалов [2] | - случай 1+2.1 (h-); |
| ЛНФ- и ПНФ-преобразования5 | - случай 1+2.2 (h-); |
| LD- и RD- преобразования | - случай 1+2.2 (h-). |
|
|
4Нерекурсивным называется нетерминал A, для которого не существует выводов вида A =>+ αAβ.
5ЛНФ-преобразование (ПНФ-преобразование) [2] заключается в устранении явно указанных общих префиксов (суффиксов) в правых частях нетерминалов.
|
|
Особого разговора заслуживает порядок размещения эквивалентных
преобразований в универсальной схеме. С точки зрения свойств конечного
результата порядок не играет роли, однако иногда частные преобразования
имеет смысл выполнять раньше общих преобразований.
Так, в некоторых случаях ЛНФ-преобразования [2] можно рассматривать как
частный случай LD-преобразований. Если, например A-правила грамматики имеют
вид
A → aB | aCc | aBAd,
то ЛНФ-преобразование терминала A совпадает с LD-преобразованием
относительно LD(a) = { A }. Вместе с тем ЛНФ-преобразование способно
обрабатывать случаи. когда все правые части A-правил начинаются одним и тем
же нетерминалом. При этом ЛНФ-преобразование действует вполне "разумно",
преобразуя
A → Bb | BCc | BaAd в A' → b | Cc | aBA'd.
LD-преобразование в этом случае действует более "топорно", преобразуя
A → Bb | BCc | BaAd в A' → B'b | B'Cc | B'abA'd .
Заключение
Настоящая работа носит исключительно теоретический характер, ее главная цель
- расширить спектр возможностей при выдвижении гипотез о строении
неизвестной грамматики, породившей некоторые известные предложения. Если,
например, известно, что LL(1) грамматика породила два предложения abcabdd и
abcbcddd, то с определенными оговорками можно считать, что оба эти
предложения в искомой грамматике имеют общую сентенциальную форму abcA"dd.
В самом деле:
- быть LL(1) означает наличие общей формы abcA, где A → abdd | bcddd, в общем виде известной как "дерево суффиксов" [3];
- доказанная допустимость RD-преобразований фактически означает наличие общей формы abcA''dd, где A'' → ab | bcd.
Упомянутые оговорки будут раскрыты в следующих работах.
Список литературы
- Ахо А., Ульман Дж. Теория синтаксического анализа,
перевода и компиляции. тт. 1,2. - М.: Мир, 1978.
- Соловьев С.Ю. Нормализация контекстно-свободных грамматик
для целей грамматического вывода. // XII национальная конференция
по искусственному интеллекту с международным участием КИИ-2010.
Труды конференции. - М.: Физматлит, 2010, том 1, стр.218-224.
- Смит Б. Методы и алгоритмы вычислений на строках. - М.: Вильямс, 2006.
|
|
|
- Точная ссылка на статью:
- Соловьев С.Ю.
- Эквивалентные преобразования контекстно-свободных грамматик.
- // Информационные процессы. Том 10, No.3, 2010. стр. 292-302.
- http://www.jip.ru
Статья размещена автором на сайте
www.glossary.ru
- Служба тематических толковых словарей
|
П|р|о|д|о|л|ж|е|н|и|е ►
|
|