Глава IV
МЕТОДЫ ВОССТАНОВЛЕНИЯ ФОРМАЛЬНЫХ ГРАММАТИК
 4.1 Постановка задачи грамматического вывода
4.1 Постановка задачи грамматического вывода
 4.2 Структура контекстно-свободных языков
4.2 Структура контекстно-свободных языков
Нормальные контекстно-свободные грамматики •
П-сети • Структура КС-языков
 4.3 Метод обобщения
4.3 Метод обобщения
 4.4 Методы структурирования
4.4 Методы структурирования
Восстановление регулярных языков •
Восстановление однозначных контекстно-свободных языков •
Эвристический метод восстановления контекстно-свободных языков
| |
Веб-версия диссертации размещена автором на www.park.glossary.ru.
Копии веб-версии на иных сайтах заведомо получены и размещены с нарушением
авторских прав, без согласия и без отвественности автора. |
В первой главе указывалось, что автоматизированные системы
инженерии знаний ориентированы на извлечение знаний путем опроса
эксперта, однако сказанное не означает принципиальный отказ от
использования методов индуктивного вывода, которые составляют
необходимый арсенал средств при анализе протоколов.
При реализации в АСИЗ блоков анализа протоколов часто приходится решать
задачу построения (восстановления) формальной грамматики по известному
множеству, порожденных ею предложений. В литературе [47] эта задача известна
как задача грамматического вывода. Для того, чтобы получить в свое
распоряжение конструктивные, математически обоснованные методы восстановления
грамматик, прежде всего необходимо привести формальную постановку задачи
грамматического вывода.
В настоящей главе предлагаются методы восстановления, состоящие из двух
стандартных этапов. Причем подзадачи, решаемые на каждом из этих этапов,
относительно независимы друг от друга.
4.1 Постановка задачи грамматического вывода
Для удобства последующего изложения, следуя [4], приведем основные понятия
теории формальных грамматик и примем ряд связанных с ними стандартных обозначений.
Алфавитом называется любое конечное множество символов.
Конечная последовательность символов
a1a2...ak,
где ai ∈ Σ Σ, (i=1,2,...,k),
называется цепочкой в алфавите Σ.
Длина последовательности называется длиной цепочки;
длину цепочки x будем обозначать |x|.
Пустой называется цепочка длины 0. Пустую цепочку будем
обозначать символом e (|e| = 0).
Пусть x - цепочка в некотором алфавите. Для любого целого i
(i ≥ 0) определим цепочку xi следующим образом:
x0 = e, xi = xxi-1
Обозначим Σ* - множество всех цепочек в алфавите Σ,
включая пустую цепочку, а Σ+ = Σ* \ {e}.
Контекстно-свободной грамматикой (КС-грамматикой) называется четверка
G = < N, Σ, P, S >, где
N - алфавит нетерминальных символов (нетерминалов);
Σ - непересекающийся с N алфавит терминальных символов (терминалов);
P - конечное множество правил вывода вида A → α, где
A ∈ N, α ∈ (N ∪ Σ)*;
S - выделенный символ из N, называемый начальным символом.
Примем следующие соглашения относительно обозначений
символов и цепочек, связанных с грамматиками:
(а) a, b, c, ... и цифры 0, 1, 2, ... обозначают терминалы;
(б) A, B, C, ... - обозначают нетерминалы; S - начальный символ;
(в) X, Y, Z - обозначают либо терминалы, либо нетерминалы;
(г) α, β, γ - обозначают цепочки, которые могут содержать
как терминалы, так и нетерминалы;
(д) u, v, w, x, y, z - обозначают цепочки, состоящие только из терминалов.
С учетом принятых соглашений грамматику
можно задавать множеством правил вывода.
Пусть G = < N, Σ, P, S > - КС-грамматика. Правила из P,
у которых левая часть есть нетерминал A, называются A-правилами.
Множество всех правых частей A-правил из P обозначим R(G,A),
R(G,A) = { α | A → α ∈ P }.
Запись A → R, где R есть множество цепочек
{ α1 , ..., αn },
будем понимать как сокращенную запись множества правил вывода
{ A → α1 , ..., A → αn }.
Пусть G = < N, Σ, P, S > - КС-грамматика. На множестве цепочек
(N ∪ Σ)* определим бинарное отношение непосредственной
выводимости =>G следующим образом:
α =>G β тогда и только тогда, когда
α = γ1Aγ2 ,
β = γ1β1γ2 и
A → β1 ∈ P.
Цепочка α называется выводимой в грамматике G,
если S =>*G α.
Каждому выводу цепочки α однозначно соответствует дерево вывода.
Язык, порождаемый грамматикой G (обозначается L(G)), есть
множество терминальных цепочек
{ x ∈ Σ* | S =>*G x }.
Цепочки языка L(G) называются предложениями.
Две грамматики называются эквивалентными,
если порождаемые ими языки совпадают.
Вывод цепочки α в грамматике G = < N, Σ, P, S >
S = α0 =>G α1 =>G ... =>G αk = α
называется левым выводом, если каждый переход
αi =>G αi+1
(i = 0, ..., k-1) можно представить в виде
αi = xAγ,
αi+1 = xβγ
(x ∈ Σ*)
и A → β ∈ P
КС-грамматика G называется однозначной, если для каждого
предложения из L(G) существует единственный левый вывод.
КС-грамматика называется праволинейной, если все ее правила
вывода имеют вид A → xB или A → x, где A и B - нетерминалы,
x ∈ Σ*. 
Задача грамматического вывода рассматривается в связи с функционированием
некоторой абстрактной системы, состоящей из источника и анализатора.
Источник - это некоторое устройство, которое располагает
языком Lи (языком источника). На каждом такте своей работы
источник передает одно новое слово из Lи на вход анализатора.
Фактически источник формирует (вообще говоря - бесконечную)
последовательность множеств {Ωi | i ≥ 1},
где Ωi состоит из
предложений, переданных на первом, втором, ..., i-м тактах.
Каждое множество Ωi называется образцом.
Анализатор - это устройство, которое на i-м такте своей
работы по образцу Ωi строит конечное
множество грамматик Gi
(множество решающих грамматик). При этом анализатор применяет к
образцу алгоритм (метод) восстановления M.
Определение.
Задача грамматического вывода называется разрешимой для
языка источника Lи, последовательности
образцов {Ωi | i ≥ 1} и
метода восстановления M, если существует число n, при котором
множество решающих грамматик Gn,
полученное из образца Ωn
методом М, содержит грамматику Gи
такую, что L(Gи) = Lи. 
В дальнейшем будем рассматривать только бесконечные языки
источника, поскольку для конечных языков сформулированная задача
грамматического вывода решается тривиально.
Возможность решения задачи грамматического вывода существенно зависит от
свойств последовательности образцов. Не останавливаясь на типологии
существующих подходов [33], сориентируемся на так называемые полные
положительные последовательности образцов.
Определение.
Последовательность образцов {Ωi | i ≥ 1}
называется полной положительной, если для
любого j ≥ 1 существует m = m(j,Lи) такое, что
{ x ∈ Lи | |x| ≤ j } ⊂ Ωm.

Основу задачи грамматического вывода составляет метод построения множества
решающих грамматик по известному образцу
Ω = Ωi. Переходя к описанию методов
восстановления, отметим,
что практически все они представляют собой комбинацию двух
самостоятельных процедур: метода структурирования и метода
обобщения. Метод структурирования по известному образцу Ω строит
конечную структуру, порождающую элементы Ω. Метод обобщения
преобразует структуру образца таким образом, чтобы она порождала
и некоторые другие предложения.
Ориентируясь на свойства последовательности образцов, методы восстановления
грамматик разрабатываются в расчете на некоторый класс языков источника.
В этом смысле можно говорить о задаче восстановления языков заданного типа.
Ниже рассматриваются методы восстановления контекстно-свободных языков.
4.2 Структура контекстно-свободных языков
Зачастую в задачах преобразования данных используют некоторое промежуточное
представление, при посредничестве которого изначально сложная задача
распадается на две простые. Следуя этому принципу, построим формальную
структуру, занимающую промежуточное положение между КС-грамматиками и
КС-языками.
Каждый КС-язык порождается некоторой КС-грамматикой. В
интересах задачи восстановления данное утверждение предстоит
усилить и показать, что класс грамматик, порождающих КС-языки,
можно ограничить так называемыми нормальными грамматиками. В
настоящем изложении нормальные грамматики используются для
определения структуры КС-языков. Однако самое существенное
свойство нормальных грамматик состоит в том, что они определяют
класс структур взаимно однозначным образом.
4.2.1 Нормальные контекстно-свободные грамматики
Выделим некоторые характеристики КС-грамматик, которые в
дальнейшем будем рассматривать как дефекты, подлежащие устранению.
Определение [4]
Пусть G = < N, Σ, P, S > - КС-грамматика.
Правило вывода вида A → e называется e-правилом.
Правило вывода вида A → B называется цепным правилом.
Правило A → α называется бесполезным,
если в грамматике G не существует вывода вида
S =>*G xAz
=>G xαz
=>*G xyz 
Определение.
Нетерминал A КС-грамматики G называется простым, если
||R(G,A)|| = 1. 
Перейдем к определению еще одного свойства КС-грамматик.
Будем рассматривать разбиения K множества нетерминалов
КС-грамматики G = < N, Σ, P, S >.
K = { KC | C ∈ N'}.
(Здесь в качестве индексов используются символы некоторого алфавита N'.)
Каждое разбиение K порождает
(а) функцию h K : N → N' такую, что h K(A) = C, если A ∈ K C;
(б) преобразование H K
цепочек из (N ∪ Σ) * и правил вывода из P:
(б') если α = y0A1y1...Amym,
то HK(α) = y0hK(A1)y1 ...hK(Am)ym;
(б'') если правило p имеет вид A → α,
то HK(p) есть hK(A) → HK(α);
(в) КС-грамматику G K = < N', Σ, H K(P), h K(S) >.
Определение 4.1
Разбиение нетерминалов КС-грамматики G = < N, Σ, P, S >
называется согласованным, если для любых нетерминалов A и B равенство
hK(A) = hK(B)
имеет место тогда и только тогда, когда для любого A-правила
A → x0A1x1...Anxn
существует B-правило
B → x0B1x1...Bnxn
такое, что
hK(A1) = hK(B1),
..., hK(An) = hK(Bn). 
Лемма 4.2
Если K - согласованное разбиение множества нетерминалов
КС-грамматики G, то L(G) = L(GK).
Доказательство. Зафиксируем некоторое согласованное разбиение K
произвольной КС-грамматики G = < N, Σ, P, S >.
Для сокращения записи введем более компактные обозначения: h = hK,
H = HK, G' = GK = < N',Σ,P',C' >.
Рассмотрим произвольное предложение x из L(G) и некоторый
левый вывод x в грамматике G.
α0
=>G α1
=>G ...
=>G αk-1
=>G αk = x
Покажем, что последовательность цепочек
H(α0), ..., H(αk)
есть левый вывод предложения x в грамматике G'.
По определению левого вывода α0 = S и H(α0) = C',
то есть H(α0) - цепочка, выводимая в грамматике GK.
Предположим, что цепочка H(αi) выводима в грамматике G'
для некоторого i < k. По определению левого вывода для грамматики G
цепочки αi и αi+1 можно представить в виде
| αi |
= z0A1z1A2z2...Amzm
|
| αi+1 |
= z0x0B1x1 ... Bnxnz1A2z2...Amzm ,
|
где A1 → x0B1x1...Bnxn ∈ P.
По определению грамматики G' имеем
h(A1) → x0h(B1)x1...h(Bn)xn ∈ P'.
Следовательно,
H(αi) = z0h(A1)z1h(A2)z2...h(Am)zm
=>G'
z0x0h(B1)x1...h(Bn)xnz1h(A2)z2...h(Am)zm
= H(αi+1).
То есть цепочка H(αi+1) также выводима в G'. Учитывая, что
H(αk) = αk = x, окончательно получаем:
x ∈ L(G') и L(G) ⊂ L(G').
Рассмотрим произвольное предложение y из L(G') и некоторый
левый вывод y в грамматике G'.
C' = β0
=>G' β1
=>G' ...
=>G' βk-1
=>G' βk = y
Построим левый вывод
α0 =>G
α1 =>G
... =>G
αk-1 =>G
αk = y
Положим α0 = S, при этом h(S) = C'.
Предположим, что удалось построить вывод
α0 =>G
α1 =>G ...
=>G
αi (i < k)
причем αi = z0A1z1A2z2...Amzm,
βi = z0C1z1C2z2...Cmzm,
h(A1) = C1, ..., h(Am) = Cm.
Как следует из определения левого вывода, в грамматике G' существует правило
C1 → x0C'1x1...C'nxn
такое, что
βi+1 = z0x0C1x1...Cnxnz1C2z2...Cmzm .
Для этого правила, согласно определению множества P', в
грамматике G существует, по-крайней мере, одно "родительское" правило
B1 → x0B'1x1...B'nxn
такое, что h(B1) = C1,
h(B'1) = C'1, ...,
h(B'n) = C'n.
Поскольку h(A1) = h(B1) = C1,
то из определения согласованного разбиения следует,
что в грамматике G существует также правило
A1 → x0A'1x1...A'nxn
такое, что h(A'1) = h(B'1) = C'1, ..., h(A'n) = h(B'n) = C'n.
Таким образом, αi =>G αi+1,
где αi+1 построению есть
цепочка z0x0A'1x1...A'nxnz1A2z2...Amzm,
в которой h(A'1) = C'1, ..., h(A'n) = C'n,
h(A2) = C2, ..., h(An) = Cn.
Следовательно α0 =>+G αi+1.
Сравнивая цепочки αi и βi,
а также, учитывая, что для i = k имеет место равенство m = 0,
получаем: αk = βk = y.
Итак, y ∈ L(G) и L(GK) ⊂ L(G). 
Следствие.
Если G - праволинейная грамматика, то GK - также
праволинейная грамматика.
Если G - однозначная КС-грамматика, то GK - также
однозначная КС-грамматика. 
Определение.
КС-грамматика G = < N, Σ, P, S > называется избыточной, если
существует согласованное разбиение нетерминалов K такое,
что ||K|| < ||N||. 
Проверка грамматики G на избыточность сводится к перебору и
оценке на согласованность всевозможных разбиений нетерминалов,
удовлетворяющих условию ||K|| < ||N||. При обнаружении такого
разбиения, грамматику G можно преобразовать к виду GK, а затем и
применить к GK ту же процедуру проверки-преобразования. В конце
концов, на некотором шаге этого итеративного процесса будет
построена неизбыточная грамматика G' эквивалентная G.
Корректность описанной процедуры устранения избыточности следует
из того, что на каждой итерации множество нетерминалов
сокращается по-крайней мере на один символ.
В данном случае процедуры преобразования грамматик интересуют нас только в
качестве средства для доказательства факта существования грамматик с заданными
свойствами.
Определение 4.3
КС-грамматика G = < N, Σ, P, S >
называется нормальной (или НКС-грамматикой), если
(а) в P имеется правило S → #, причем в остальных правилах вывода терминал # не встречается;
(б) в P отсутствуют e-правила, за исключением, быть может, правила S → e;
(в) в P отсутствуют цепные правила;
(г) в P отсутствуют бесполезные правила;
(д) в N отсутствуют простые нетерминалы;
(е) G не является избыточной грамматикой.  Теорема.
Для любой КС-грамматики G существует HKC-грамматика Gн такая,
что L(Gн) = L(G) ∪ {#}, где # - новый для грамматики G
терминальный символ.
Доказательство. Существует цепочка преобразований исходной
грамматики к искомому виду.
G  Gа
Gа  Gб
Gб  Gв
Gв  Gг
Gг  Gд
Gд  Gе = Gн
Gе = Gн
В данной цепочке считается, что грамматика Gx удовлетворяет
требованиям (а)-(x) определения 4.3.
Преобразование G  Gа
определяется следующим образом:
если G = < N, Σ, P, S' >,
то Gа = < N ∪ {S}, Σ ∪ {#}, P ∪ (S → S' | #), S >,
где # и S - символы, не встречающиеся в грамматике G.
Очевидно, что L(Gа) = L(G) ∪ {#} и грамматика Gа удовлетворяет
требованию (а). Gа
определяется следующим образом:
если G = < N, Σ, P, S' >,
то Gа = < N ∪ {S}, Σ ∪ {#}, P ∪ (S → S' | #), S >,
где # и S - символы, не встречающиеся в грамматике G.
Очевидно, что L(Gа) = L(G) ∪ {#} и грамматика Gа удовлетворяет
требованию (а).
Преобразования
Gа  Gб,
Gб Gб,
Gб  Gв,
Gв Gв,
Gв  Gг,
Gг Gг,
Gг  Gд,
хорошо изучены [4]. В частности, известно, что
каждое из этих преобразований Gд,
хорошо изучены [4]. В частности, известно, что
каждое из этих преобразований
(1) сохраняет результаты ранее выполненных преобразований,
(2) является эквивалентным преобразованием КС-грамматик,
(3) сохраняет однозначность и праволинейность грамматики.
Преобразование
Gд  Gе
реализует описанная выше процедура устранения избыточности. Очевидно, что
эта процедура не отменяет свойства (а)-(д). Gе
реализует описанная выше процедура устранения избыточности. Очевидно, что
эта процедура не отменяет свойства (а)-(д). 
Следствие.
Для любой однозначной (праволинейной) КС-грамматики G
существует однозначная (праволинейная) HKC-грамматика Gн такая,
что L(Gн) = L(G) ∪ {#},
где # - некоторый новый терминальный символ. 
Требование (а) из определения 4.3 позволяет упростить
теоретические рассуждения по поводу особых свойств начального
символа грамматики. Правило S → # из Gн всегда можно исключить,
получив при этом остаточную грамматику эквивалентную G.
4.2.2 П-сети
Определение структуры КС-языков существенно использует
аппарат П-сетей [51] специального вида.
Определение.
Двухполюсной сетью называется четверка < M, W, p, q >, где
| (a) |
M - множество вершин;
|
| (б) |
W - множество ориентированных ребер вида (m,m')X,
причем метка ребра X есть символ некоторого алфавита;
|
| (в) |
p и q - выделенные вершины из M, которые называются
соответственно входным и выходным полюсами сети. Вершины,
отличные от полюсов, называются внутренними. 
|
В сетях с помеченными ребрами каждому пути
[m0,mk] =
(m0,m1)Y1
(m1,m2)Y2 ...
(mk-1,mk)Yk
однозначно соответствует цепочка меток
α = Y1Y2...Yk.
Будем использовать обозначение
[m0,mk]α
в качестве краткого эквивалентна предыдущей фразы.
Определение 4.4
Сеть T = < M, W, p, q > с помеченными ребрами порождает язык
L(T) = { α | [p,q]α - путь в T }.
Сеть T называется однозначной, если для любых различных
путейя [p,q]α и [p,q]β
имеет место неравенство α ≠ β. 
Определение.
Подсетью сети T = < M, W, p, q > будем называть сеть
T' = < M', W', p, q > такую, что
(1) M' ⊂ M, W' ⊂ W;
(2) для любого ребра из W' в сети T' существует путь [p,q],
проходящий через это ребро. 
Если в сети зафиксировать некоторое количество путей,
соединяющих полюса, то вершины и ребра, входящие в эти пути,
однозначно определяют некоторую подсеть.
Будем рассматривать взаимно однозначные функции переименования вершин
r : M → M'.
Для единообразия обозначений будем считать, что r(W) есть множество
{ (r(m), r(m'))a | (m, m')a ∈ W}.
Определение.
Сети < M, W, p, q > и < M', W', p', q' > будем называть
изоморфными, если существует функция переименования
r : M → M' такая, что r(p) = p', r(q) = q' и r(W) = W'. 
Другими словами, под изоморфизмом сетей понимается
такой изоморфизм, который сохраняет разметку ребер.
Определение.
Однореберная двухполюсная сеть
< {p,q}, {(p,q)a}, p, q > является П-сетью.
Если
< M1, W1, p1, q1 > и
< M2, W2, p2, q2 > - П-сети,
то
и s-сеть < M1 ∪ rs(M2), W1 ∪ rs(W2), p1, rs(q2) >,
и p-сеть < M1 ∪ rp(M2), W1 ∪ rp(W2), p1, q1 >
являются П-сетями для любых функций переименования
rs и rp : M2 → M'2,
удовлетворяющих условиям:
(а) rs(p2) = q1 и
M1 ∩ rs(M2) = {q1};
(б) rp(p2) = p1,
rp(q2) = q1 и
M1 ∩ rp(M2) = {p1,q1}. 
Соглашение.
В теоретических построениях, связанных с определением структуры КС-языков,
будем предполагать, что вершины П-сетей задаются цепочками некоторого алфавита.
При этом можно считать, что ребра также представляют собой цепочки символов.
Скажем, ребру вида (α,β)a соответствует цепочка
(α,β,a) в алфавите, дополненном символами "(", "," и ")". 
Определение.
Пусть T = < M, W, p, q > - сеть, и W ' - выделенное подмножество
ребер из T. Кроме того, известно соответствие, по которому
ребрам w из W ' однозначно сопоставляются некоторые П-сети
< Mw, Ww, pw, qw gt;.
Результатом подстановки в сеть T вместо ребер из
W ' соответствующих П-сетей называется двухполюсная сеть
< Mres, Wres, p, q >, в которой
| Mres = |
∪ |
rw(Mw) ∪ M, |
|
w ∈ W ' |
|
|
| Wres = |
∪ |
rw(Ww) ∪ W \ W ' |
|
w ∈ W ' |
|
|
и каждая функция переименования вершин сети Tw для
w = (a,b)x есть:


При некоторых условиях операция подстановки позволяет
синтезировать новые П-сети из более простых элементов. Введем
ряд специфических определений и обозначений, позволяющих
анализировать структуру П-сетей.
В П-сети T = < M, W, p, q > выделим пару вершин p' и q' и
обозначим через T(p',q') четверку < M', W', p', q' >, в которой M' и
W ' составляют вершины и ребра сети T, принадлежащие хотя бы
одному пути [p',q'].
Определение 4.5
Будем говорить, что пара вершин p' и q' определяет p-элемент сети
T = < M, W, p, q >, если T(p',q') является p-сетью, и любой путь
[p,q], содержащий внутренние вершины сети T(p',q'), проходит через p' и q'.

На p-элементах естественным образом определяется отношение вложенности.
Определение.
Будем говорить, что p-элемент T(p',q') вложен в p-элемент
T(p'',q''), и писать T(p',q') ⊂ T(p'',q''), если все вершины
первой сети являются вершинами второй сети. 
Отношение вложенности порождает древовидную иерархию Д(T)
p-элементов сети T. Корнем дерева Д(T) является сама сеть T.
Вершинами дерева Д(T) являются p-элементы сети T.
Обозначим inn(T') - множество p-элементов, непосредственно
вложенных в p-элемент T'.
Иерархия вложенности позволяет однозначно приписать
значение глубины каждому p-элементу p-сети T. По определению
глубина p-элемента T' есть глубина вершины T' дерева Д(T).
Пример.
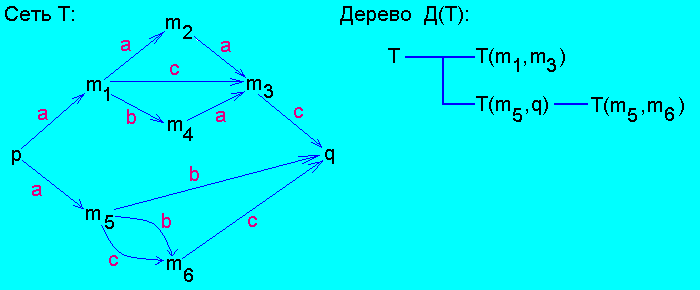
L(T) = {ab, abc, acc, aaac, abac}.
Сеть T не является однозначной.
| inn(T) = {T(m1,m3),T(m5,q)} |
глубина(T) = 0 |
| inn(T(m1,m3)) = ∅ |
глубина(T(m1,m3)) = 1 |
| inn(T(m5,q)) = {T(m5,m6)} |
глубина(T(m5,q)) = 1 |
| inn(T(m5,m6)) = ∅ |
глубина(T(m5,m6)) = 2 |

Из определения 4.5 следует, что в любой П-сети T можно выполнить замену
p-элемента T(p',q') на некоторое ребро (p',q')x. Сеть, полученная
в результате такой замены, по-прежнему остается П-сетью.
Определение.
Пусть T - р-сеть и n - некоторое число. Будем обозначать
П(T,n) П-сеть, которая получается из T заменой всех ее
p-элементов T(p',q') глубины n на ребро (p',q')П, помеченное
уникальным фиксированным символом П. 
На содержательном уровне можно говорить, что сеть П(T,n)
сохраняет внешнюю структуру сети T, а на местах несущественных
деталей располагаются ребра-заглушки, помеченные специальным символом П.
Определение.
Будем полагать, что две p-сети T' и T'' связаны отношением
≈n, и писать T' ≈n T'',
если p-сети П(T',n) и П(T'',n) изоморфны. В случае, когда сети
T1 и T2 не связаны отношением ≈n,
будем писать
T1  T2. T2.

4.2.3 Структура КС-языков
Рассмотрим вопрос о соотношении КС-языков и П-сетей.
Определение.
Пусть G = < N, Σ, P, S > - НКС-грамматика.
НКС-диаграммой tA,0
(A ∈ N) называется П-сеть
< MA,0, WA,0, pA, qA > вида:
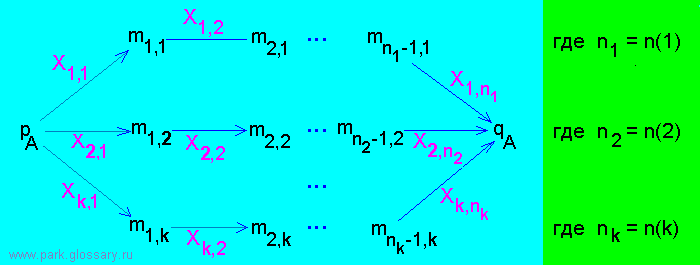 где L(tA,0) = { Xi,1Xi,2...Xi,n(i) | i = 1, ..., k } = R(G,A),
где L(tA,0) = { Xi,1Xi,2...Xi,n(i) | i = 1, ..., k } = R(G,A),
а множество вершин MA,0 = { pA, qA, m1,1, m2,1, ..., mn(i)-1,1, ... }
представляет собой уникальный алфавит символов, то есть
MA,0 ∩ MB,0 = ∅, если A ≠ B. 
НKC-диаграммы обладают рядом свойств.
Первое. В НКС-диаграммах отсутствуют ребра, помеченные символом e.
Исключение составляет диаграмма tS,0, которая может содержать ребро
(pS,qS)e. 
Второе. Во всех НКС-диаграммах отсутствуют ребра (pA,qA)B,
где B ∈ N. (Другими словами, если ребро НКС-диаграммы помечено
нетерминалом, то, по-крайней мере, одна из его вершин является
внутренней.) 
Третье. Все НКС-диаграммы являются p-сетями. 
Перечисленные особенности являются всего лишь переформулировкой свойств
(б), (в) и (д) определения 4.3. Остальные свойства НКС-грамматик проявляются
на сетях более сложной структуры.
Будем обозначать:
— W[A] = {(m,m')X ∈ W | X ∈ A} - множество ребер сети < M, W, p, q >,
помеченных символами из алфавита A;
— VA = WA,0[N];
— tw,1 = tA,1, Mw,1 = MA,1, .... ,
если ребро w помечено символом A.
Определение 4.6
Определимя для НКС-грамматики G = < N, Σ, P, S > семейство сетей
{ tA,1 | A ∈ N, i ≥ 0 }
следующим образом: для i ≥ сеть
tA,i+1 = < MA,i+1, WA,i+1, pA, qA >
есть результат подстановки в
НКС-диаграмму tA,0 вместо каждого ребра w ∈ VA
соответствующей ему сети tw,i. 
В связи с определением 4.6 индукцией по i легко показать,
что (при i ≥ 0 и A ∈ N)
- произвольная сеть tA,i принадлежит классу p-сетей;
- inn(tA,i+1) = { rw(tw,1) | w ∈ VA }
(Откуда следует, что в сети tA,i любой p-элемент глубины k
изоморфен сети tB,i-k для некоторого B из N.);
- MA,i ⊂ MA,i+1 и WA,i[Σ] ⊂ WA,i+1[Σ];
- L(tA,i) = L(G,A,i) ∪ L(G,A,i),
где
- L(G,A,i) - содержит все терминальные цепочки из
{ x | A =>*G x },
которым соответствуют деревья вывода глубины не более i+1;
- L(G,A,i) - содержит все цепочки из
{ αBβ | A =>*G αBβ, B ∈ N },
которым соответствуют деревья вывода глубины i+1.
Определение 4.7
Для каждого нетерминала A НКС-грамматики определим сеть
TA =
< MA, WA, pA, qA >,
в которой
Приведем свойства сетей TA:
| — inn(TA) = |
{ rw(Tw) | w ∈ VA };
|
| — L(TA) = |
∪ |
LA,i = { x | A =>G x } и, в частности, L(TS) = L(G). |
|
i ≥ 0 |
|
Таким образом, сеть TS можно рассматривать, как структуру
КС-языка.
Замечание.
Если G - однозначная НКС-грамматика, то все сети TA и
tA,i являются однозначными. 
Лемма 4.8
Для любой НКС-грамматики G = < N, Σ, P, S > сети из множества
{ TX | X ∈ N } попарно неизоморфны.
Доказательство. Предположим, что в некоторой НКС-грамматике
G, по-крайней мере, для двух нетерминалов X и Y сети TX
и TY
изоморфны. Построим для этой грамматики разбиение нетерминалов K
следующим образом: нетерминалы A и B относятся к одному классу
KC тогда и только тогда, когда сети
TA и TB изоморфны. По
предположению ||K|| < ||N||.
Докажем, что разбиение K является согласованным.
Зафиксируем две произвольные изоморфные две сети TA и TB.
Обозначим h - взаимно однозначное соответствие MA → MB,
поддерживающее этот изоморфизм. Тогда
h(MA,0) = MB,0.
(Если предположить, что для некоторой вершины mA ∈ MA,0
вершина mB = h(mA) не принадлежит MB,0,
то mB является внутренней вершиной
для некоторой сети rw(Tw),
причем {pw,qw} ≠ {pB,qB}.
В силу изоморфизма вершина mA = g(mB),
где g = h-1, также является внутренней вершиной некоторого p-элемента
TA(g(pw),g(qw)),
причем {g(pw),g(qw)} ≠
{g(pB),g(qB)} = {pA,qA}.
То есть mA ∉ MA,
что противоречит сделанному предположению.)
Рассмотрим свойства взаимно однозначного соответствия h
применительно к НКС-диаграммам tA,0 и tB,0.
| (1) |
Если w = (a,b)X ∈ WA,0,
то h(w) = (h(a),h(b))Y ∈ WB,0 для некоторого Y.
|
| (2) |
Если X ∈ Σ, то Y = X. |
| (3) |
Если X ∈ N, то Y ∈ N, причем
сеть rw(TX) изоморфна сети rh(w)(TY), то есть
сеть TX изоморфна сети TY , то есть
X и Y принадлежат одному классу из K.
|
Свойства (1)-(3) гарантируют согласованность разбиения K (см.
определения 4.1 и 4.4).
Таким образом, грамматика G является избыточной, что не
соответствует определению НКС-грамматик. 
Следствие.
Для любой НКС-грамматики G существует число E(G) > 0 такое,
что при j ≥ i ≥ E(G) сети множества
{ П(tX,j,i) | X ∈ N }
попарно неизоморфны. 
Для заданной НКС-грамматики определим семейство П-сетей
{ TS,i | i ≥ 1}.
Поскольку НКС-грамматика не содержит бесполезных правил
вывода, то для любого i ≥ в сети TS существует класс
П-подсетей T, удовлетворяющих свойству T ≈i tS,i.
Обозначим TS,i наименьшую (по числу ребер) сеть из этого класса.
(В случае нескольких наименьших сетей выбираем одну из них.)
4.3 Метод обобщения
Следствие из леммы 4.8 позволяет надеяться, что для восстановления
НКС-грамматики можно ограничиться некоторой подсетью TS,i.
Покажем это.
Определение.
Пусть G = < N, Σ, P, S > - НКС-грамматика, n = E(G). Определим
два класса П-сетей U(G) и UU(G), а также функцию u : U(G) → N.
| (1) |
П-сеть T принадлежит классу U(G) тогда и только тогда, когда
T ≈n tA,n для некоторого A = u(T).
|
| (2) |
UU(G) = { T ∈ U(G) | inn(T) ⊂ U(G) }. |
Базисом множества U(G) будем называть подмножество
Б ⊂ UU(G) такое, что u(Б) = N и ||Б|| = ||N||.

Базисами множества U(Б) являются, в частности, множества
{ TX | X ∈ N },
{ TX,i | X ∈ N },
{ П(tX,j,i) | X ∈ N }
(для j ≥ i > E(G)).
Нас будут интересовать функции именования f: U(G) → N',
удовлетворяющие условию f(T) = f(T'), если T ≈n T' (n = E(G)).
Для того, чтобы построить функцию именования достаточно задать
ее значения на некотором базисе, а затем доопределить ее с
помощью отношения ≈n. При таком подходе вычисление
функции сводится к проверке на изоморфизм конечных П-сетей.
Поскольку функции именования однозначно определяют классы
эквивалентности отношения ≈n,
то все эти функции эквивалентны друг другу с точностью до взаимно
однозначного переименования множества значений. Поэтому в дальнейшем
изложении будем использовать только одну функцию именования - функцию u.
При этом все равенства цепочек справедливы с точностью до взаимно
однозначного переименования нетерминалов.
Определение 4.9
Пусть G = < N, Σ, P, S > - НКС-грамматика, n = E(G), Б - базис
класса U(G), T - сеть из UU(G). Определим:
— сеть t(u,T) как результат подстановки в сеть T вместо
p-элементов T(m,m') ∈ inn(T) соответствующих ребер
(m,m')X, где X = u(T(m,m'));
— множество правил вывода P(u,Б), задающих грамматику G(u,Б),
| P(u,Б) = |
∪ |
(u(T) → L(t(u,T))). |
|
T ∈ Б |
|

Лемма 4.10
При условиях, заданных в определении 4.9,
имеет место равенство P = P(u,Б).
Доказательство. Поскольку Б - базис класса U(G), то
| P(u,Б) = |
∪ |
(X → L(t(u,TX))), где TX ∈ Б и u(TX) = X. |
|
X ∈ N |
|
Рассмотрим сеть tX,n+1.
inn(tX,n+1) = { rw(tY,n) |
w = (a,b)Y ∈ VX}.
Учитывая, что
u(rw(tY,n)) = u(tY,n) = Y,
из определения 4.9 для ребер сети t(u,tX,n+1) получаем выражение
WX,0[Σ] ∪ {(m,m')Y | w = (m,m')Y ∈ VX}
=
WX,0[Σ] ∪ VX
=
WX,0.
То есть t(u,tX,n+1) = tX,0.
По определению класса UU(G) между сетями П(tX,n+1,n+1) и
П(TX,n+1) существует отношение изоморфизма, которое, в частности,
индуцирует изоморфизм сетей t(u,tX,n+1) и t(u,TX).
Следовательно, L(t(u,TX)) = L(tX,0) = R(G,X).
Таким образом:
| P(u,Б) = |
∪ |
(X → R(G,X)) = P. |
|
X ∈ N |
|

Покажем, что базис класса U(G) можно построить по конечному
фрагменту сети TS.
Определение 4.11
Пусть T - П-сеть и n - некоторое число. Определим
подмножество p-элементов Ф(T,n), удовлетворяющее трем условиям.
| (1) |
T ∈ Ф(T,n). |
| (2) |
Если T' и T'' - пара различных сетей из Ф(T,n), то T' ≈n T''.
|
| (3) |
Если T'' ∈ inn(T') и T' ∈ Ф(T,n), то либо T'' ∈ Ф(T,n),
либо T'' ≈n TB, для некоторой сети TB ∈ Ф(T,n).
|

Свойства (1) и (3) определяют множество Ф(T,n) как
некоторую "сплошную" окрестность корня дерева Д(T). Очевидно,
что по заданным T и n можно построить, по-крайней мере, одно
множество Ф(T,n).
Лемма 4.12
Пусть G = < N, Σ, P, S > - НКС-грамматика, n = E(G) и
T - некоторая П-сеть такая, что T ≈i tS,i
при i > ||N||+n
Тогда Ф = Ф(T,n) есть базис класса U(G).
Доказательство. Поскольку в определении множества Ф(T,n)
используется только отношение изоморфизма, то искомое
утверждение достаточно показать для T = tS,i.
В обозначениях p-элементов будем использовать [первые] нижние
индексы, совпадающие со значениями глубины соответствующих
p-элементов. Кроме того, обозначим
V = { T'k - p-элемент сети T | k ≤ ||N|| }
Последовательно докажем следующие утверждения:
(1) V ⊂ UU(G);
(2) Ф ⊂ V;
(3) u(Ф) = N;
(4) ||Ф|| = ||N||.
(1) В соответствии со свойствами сети tS,i каждая сеть
T' ∈ V изоморфна некоторой сети tA,i-k. Откуда следует, что
T'k ≈i-k tA,i-k, причем i-k > n.
Последнее неравенство гарантирует, что V ⊂ UU(GG).
(2) Положим n' = ||N|| и рассмотрим произвольный p-элемент
T'n' и связанную с ним последовательность вложенных p-элементов
T'n' ⊂ ... ⊂ T'1 ⊂ T'0 = T
Перекодируем эту последовательность с помощью функции u:
An', ... , A1, A0 (A0 = S)
Поскольку членами последовательности являются нетерминалы из
алфавита N, то в ней обязательно найдутся, по-крайней мере, два
совпадающих нетерминала Ak' и Ak" (n' ≥ k' > k"). То есть
T'k ∉ Ф для k = k' , ..., n'.
(3) Предположим, что существует непустое множество нетерминалов
N' = N \ f(Ф). По определению множества Ф(T,n) S ∉ N'.
Зафиксируем некоторый нетерминал A ∈ N'. Поскольку
НКС-грамматика не содержит бесполезных правил, то существует
p-элемент T'k ∈ V такой, что u(T'k) = A.
Рассмотрим последовательность непосредственно вложенных p-элементов
T'k ⊂ ... ⊂ T'1 ⊂ T'0 = T
Перекодируем эту последовательность с помощью функции u:
(Ak = A)
Ak, ... , A1, A0
(A0 = S)
В этой последовательности Ak ∈ N', но A0 ∉ N'.
Следовательно, наl;йдется номер j > 0 такой,
что Aj ∉ N', и Aj-1 ∈ N'.
Введем обозначения для пары смежных сетей: B = Aj-1,
TB = Tj-1,
C = Aj,
TC = Tj.
Так как B ∈ N', то существует сеть
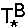 ∈ Ф
такая, что u( ∈ Ф
такая, что u(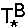 ) = B. ) = B.
Поскольку {TB,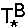 } ⊂ V ⊂ UU(G),
то TB ≈n+1 } ⊂ V ⊂ UU(G),
то TB ≈n+1 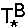 .
Этот изоморфизм однозначно сопоставляет p-элементу
TC ∈ inn(TB)
некоторый элемент .
Этот изоморфизм однозначно сопоставляет p-элементу
TC ∈ inn(TB)
некоторый элемент
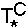 ∈ inn( ∈ inn(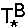 ),
причем u( ),
причем u(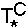 ) = C. ) = C.
Итак, имеем: 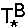 ∈ Ф, ∈ Ф,
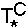 ∈ inn( ∈ inn(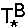 ).
По определению множества Ф среди его элементов найдется
сеть ).
По определению множества Ф среди его элементов найдется
сеть 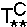 такая, что
такая, что 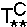 ≈n ≈n 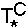 ,
то есть u( ,
то есть u(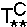 ) =
u( ) =
u( ) = C. Следовательно, ) = C. Следовательно,
C ∈ f(N) и C = Aj ∉ N'.
(4) В данном случае равенство ||Ф|| = ||N||
является следствием определения Ф(u,T) и свойств числа E(G). 
Определение 4.13
Пусть T - некоторая П-сеть.
Определим множество грамматик
G(T) = { G(fn,Фn) | n = 1, ..., глубина(T)+1 }, где
Фn = Ф(T,n) - множество сетей, удовлетворяющих определению 4.11,
fn - некоторая функция именования, заданная на Фn;
G(fn,Фn) - грамматика, построенная согласно определению 4.9. 
Теорема 4.14
Пусть G = < N, Σ, P, S > - НКС-грамматика и T - П-сеть
изоморфная некоторой сети TS,i для i ≥ ||N|| + E(G).
Тогда множество G(T)
содержит грамматику G' такую, что L(G') = L(G).
Доказательство. Прежде всего заметим, что
1 ≤ E(G) &le глубина(T)+1 и T ≈i tS,i
В соответствии с леммой 4.12 множество Фn = Ф(T,n) при n = E(G)
является базисом класса U(G). Поэтому из леммы 4.10 следует, что
грамматика G' = G(fn,Фn)
отличается от G лишь именами нетерминалов. 
Замечание.
Определение 4.13 можно рассматривать как метод вычисления
множества грамматик G(T). При таком подходе
это определение следует дополнить предварительным и заключительным
преобразованиями. Предварительное преобразование модифицирует
множество ребер сети T = < M, W, p, q >:
W = W ∪ { (p,q)# }. (Напомним, что наличие правила
S → # является обязательным свойством НКС-грамматик.)
Заключительное преобразование удаляет из построенных грамматик
G(fn,Фn) правило S → #. 
4.4 Методы структурирования
Определение 4.13 фактически задает метод обобщения для произвольных
КС-языков. В соответствии с теоремой 4.14 нас будет интересовать задача
восстановления сети TS,n (с точностью до отношения
≈n) по некоторому множеству предложений
Ω = Ωi(n),
принадлежащему полной положительной последовательности образцов. Подходы к
решению поставленной задачи определяются дополнительными ограничениями на
класс языков источника. Естественно, что самые жесткие ограничения приводят
к наиболее эффективным процедурам восстановления. Рассмотрим три метода
восстановления, ориентированные на разные подклассы КС-языков.
4.4.1 Восстановление регулярных языков
Язык является регулярным, если он порождается праволинейной грамматикой [4].
Замечание 4.15
Выберем уникальный символ ¶. Задачу восстановления
регулярных языков достаточно рассмотреть для случая
модифицированных образцов
mdf(Ω) = { x¶ | x ∈ Ωя0 },
соответствующих виртуальным языкам источника
Lи,v = { x¶ | x ∈ Lи }.
Известно [4], что существует универсальная процедура
преобразования грамматик, которая позволяет по грамматике G,
порождающей некоторый язык Lи,v, построить грамматику clr(G),
порождающую язык Lи. В общем случае, метод восстановления
регулярных языков должен включать предварительный этап
преобразования образца к виду mdf(Ω), а на заключительном этапе
все решающие грамматики необходимо привести к виду clr(G). 
Применительно к языкам Lи,v известные результаты [4] теории
регулярных языков позволяют утверждать, что
для любого языка Lи,v
существует порождающая его праволинейная грамматика Gv, в которой
| (1) |
все правила вывода имеют вид A → axB или A → ax для
некоторого x из Σ*;
|
| (2) |
для различных A-правил A → aα и A → bβ
имеет место неравенство a ≠ b.
|

Очевидно, что НКС-грамматика Gн,v, построенная по грамматике
Gv, сохраняет свойства (1) и (2). А это, в свою очередь,
позволяет сформулировать два характеристических свойства П-сети
T = TS, построенной по НКС-грамматике Gн,v.
Свойство праволинейности. Выходные полюса всех p-элементов
сети T совпадают с выходным полюсом самой сети T.
Свойство детерминированности. Любые два ребра (m,m')a и
(m,m")b, исходящие из одной вершины m, помечены различными
символами a и b, если m' ≠ m".
Свойства праволинейности и детерминированности позволяют восстановить любую
подсеть T' сети T по известному множеству цепочек Ω = L(T').
Определение 4.16
Пусть Ω - множество предложений.
Определим сеть TRL(Ω) следующим образом:
(а) множество вершин
M = { {x} | xy ∈ Ω для некоторого y ∈ Σ* } ∪ {Ω};
(а) множество ребер
W = { (m,m')a | x ∈ m ∈ M, xa ∈ m' ∈ M };
(а) входной полюс p = {e};
(а) выходной полюс q = Ω.
Если все предложения из Ω имеют концевой маркер, то сеть
TRL(Ω) (1) удовлетворяет свойству детерминированности; (2) по
сути дела, представляет собой дерево со "склеенными" концевыми
вершинами. (Отсюда, в частности, вытекает, что TRL(Ω) -
П-сеть.) Алгоритмически построение сети TRL(Ω) сводится к левой
факторизации [14] множества предложений из Ω (см. пример 5.9).
Лемма 4.17
Пусть Gн,v = < N, Σ, P, S > - праволинейная НКС-грамматика,
порождающая язык Lи,v, и Ω - подмножество предложений из Lи,v
такое, что L(TS,n) ⊂ Ω для некоторого n.
Тогда TRL(Ω) ≈n TS,n. 
Метод 4.18 (Восстановление регулярных языков).
Шаг 1 (Структурирование). По заданному образцу Ω, используя
определение 4.16, построить сеть T = TRL(Ω).
Шаг 2 (Обобщение). По сети T, используя определение 4.13, построить
множество решающих грамматик G(T). 
Теорема 4.19
Задача грамматического вывода разрешима для регулярного
языка источника Lи, полной положительной последовательности
образцов { Ωi | i ≥ 1 } и метода восстановления 4.18.
Доказательство. В силу замечания 4.15, утверждение теоремы
достаточно показать для некоторого регулярного языка источника
Lи,v. Зафиксируем такой язык и рассмотрим порождающую
его грамматику Gн,v = < N, Σ, P, S >.
Положим n = ||N|| + E(Gн,v)
и m = max { |x| | x ∈ L(TS,n) }.
Поскольку последовательность образцов является полной положительной,
то среди ее членов найдется образец Ωi(m) такой, что
L(TS,n) ⊂ { x ∈ L | |x| ≤ m} ⊂ Ωi(m).
Из леммы 4.17 следует, что TRL(Ωi(m)) ≈n TS,n.
В силу теоремы 4.14 множество G(TRL(Ωi(m))
содержит грамматику G', такую, что L(G') = L(Gн,v) = Lи,v. 
Идея использовать свойство детерминированности для
восстановления регулярных языков была впервые сформулирована в
работах Дж.Фельдмана и др. [55]. Метод 4.18 можно рассматривать
как уточненную версию метода Фельдмана, гарантирующую
восстановление однозначной грамматики.
4.4.2 Восстановление однозначных контекстно-свободных языков
В отличии от регулярных языков, при восстановлении КС-языков общего вида
приходится опираться на свойства гипотетической грамматики, порождающей язык
источника. Общий подход к восстановлению КС-языков предполагает, что класс
НКС-грамматик можно дополнительно ограничить.
Определение [4]
Нетерминал A КС-грамматики G называется рекурсивным, если
A =>+G αAβ ; в противном случае нетерминал
A называется нерекурсивным. Грамматика называется нерекурсивной, если она не
содержит рекурсивных нетерминалов. 
Методы устранения нерекурсивных нетерминалов известны [4].
Однако, в результате применения такого преобразования к
НКС-грамматике, вновь построенная грамматика может стать
избыточной. В связи с этим необходимо заново обратиться к
процедуре устранения избыточности. В дальнейшем будем
рассматривать только такие НКС-грамматики, в которых все
нетерминалы, отличные от начального, являются рекурсивными.
В терминах структуры КС-языков дополнительное ограничение
позволяет утверждать, что в любой сети TA (A ≠ S) найдется
собственный p-элемент T', изоморфный TA. В этом случае можно
рассчитывать, что некоторая конфигурация ребер, встречающаяся во
внешней структуре сети TA, будет циклически повторяться для ее
p-элементов. Будем использовать это наблюдение для
восстановления конечного фрагмента сети TS. Однако прежде
всего, построим метод выявления особых предложений языка
источника, выводимых непосредственно из начального символа.
Определение.
Пусть G = < N, Σ, P, S > - НКС-грамматика. Определим
— множество предложений
ост(G) = {x ∈ Σ* | x ∈ R(G,S), x ≠ #};
— множество правил вывода осн(P), задающих грамматику осн(G):
осн(P) = P \ (S → ост(G)). 
Напомним, что # - специальный символ НКС-грамматик.
Определим для него сеть T#, состоящую из единственного ребра
(p,q)#.
Связь между однозначной грамматикой G и соответствующей грамматикой осн(G)
очевидна: ост(G) = L(G) \ L(осн(G)). Кроме того, осн(осн(G)) = осн(G).
Определение 4.20
Пусть G = < N, Σ, P, S > - НКС-грамматика и
Ω - конечное множество цепочек. Определим
— множество предложений
ост(G,Ω) = { x ∈ Ω | x - не выводима в G };
— множество правил вывода доо(P,Ω), задающих грамматику
доо(G,Ω):
доо(P,Ω) = P ∪ (S → ост(G,Ωя0)). 
Если для однозначной НКС-грамматики G, множество Ω удовлетворяет
условию ост(G,Ω) ⊂ Ω ⊂ L(G), то G = доо(осн(G)Ω).
Перейдем к вопросу о восстановлении основной части правил НКС-грамматики.
Соглашение.
Зарезервируем символ R для обозначения множеств, элементами
которых являются пары цепочек (x,y) из некоторого алфавита.
Символом F будем обозначать множества, элементами которых
являются R-множества. 
Определение.
Пусть F = {R1,..., Rk}. Определим
— множество ребер
МР(F) = { (R,R')a &124; (x,ay) ∈ R ∈ F, (xa,y) ∈ R' ∈ F };
— предикат OK: OK(F) тогда и только тогда, когда для любых R и
R' из F существует подмножество
{ R'1, ..., R'n } ⊂ F такое, что
R'1 = R, R'n = R' и
R'i ∩ R'i+1 ≠ ∅ (i=1, ..., n-1);
— наименьшее разбиение на подмножества
НР(F) = { F1, ..., Fm }
такое, что OK(Fi) (i=1,...,m);
— множество укрупненных элементов
| МУ(F) = { |
∪ |
R | F' ∈ НР(F)}. |
|
R ∈ F' |
|

Определение.
Пусть T = < M, W, p, q > - П-сеть. Определим
— для заданной вершины m ∈ M множество
R(T,m) = { (x,y) | [p,m]x[m,q]y - путь в T };
— множество
F(T) = { R(T,m) | m ∈ M \ {p,q} }. 
Определение.
Определим сумму П-сетей
Ti = < Mi, Wi, pi, qi >
( i=1,...,n ),
будем обозначать ее ⊕{ T1 , ..., Tn },
как сеть < F, MP(F), Rвх, Rвых >, где
| (а) |
| n | |
| F= МУ({ |
∪ |
F(Ti)) ∪ { Rвх, Rвых }; |
| i = 1 | |
|
| (б) |
| n | |
| Rвх = |
∪ |
R(Ti,pi); |
| i = 1 | |
|
| (в) |
| n | |
| Rвых = |
∪ |
R(Ti,qi). |
| i = 1 | |
|

Лемма 4.21
Пусть T - однозначная П-сеть и T1, ..., Tn
- некоторое множество ее подсетей.
Тогда ⊕{ T1, ..., Tn} - П-сеть. 
В связи с грамматиками нас будут интересовать подсети простой циклической
структуры. Прежде чем перейти к определению этих сетей, договоримся обозначать
на рисунках путь [m,m']x в виде стрелки с меткой x. В случае x = e
стрелка вырождается в вершину m.
Определение.
Будем называть Л-сетью (бесконечную) сеть вида:
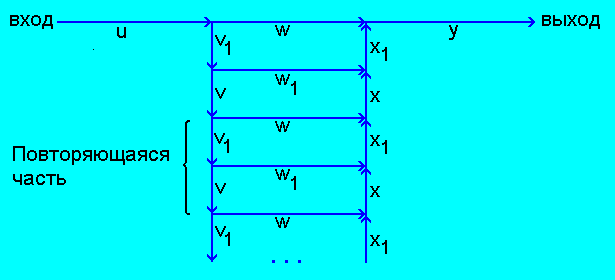
где vv1xx1 ≠ e, w ≠ e,
w1 ≠ e, uy ≠ e.
(Л-сеть можно рассматривать как "лестницу" с чередующимися "ступеньками".) 
Определение.
Пусть T = < M, W, p, q > - Л-сеть и k - некоторое целое число.
Будем обозначать [T]k конечную подсеть сети T, содержащую все
пути [p,q]x такие, что
|x| < min(
|u(v1v)kw(xx1)ky |,
|u(v1v)kv1w1x1(xx1)ky|).
Сеть, изоморфную некоторой сети [T]k, будем называть k-Л-сетью. 
Лемма 4.22
Пусть n, k - целые числа и G = < N, Σ, P, S >
- однозначная НКС-грамматика, удовлетворяющая условию G = осн(G).
Тогда существует конечное множество { T1, ... Tm}
Л-подсетей сети TS такое, что
n
⊕{ T#, [T1]k(1) ,..., [Tm]k(m) } ≈n TS,n
при min{ k(1), ..., k(m) } ≥ k.
Доказательство теоремы состоит в конструировании множества
Л-подсетей с заданными свойствами. Корректность применения
отношения ≈n к сети
⊕{ T#, [T1]k(1) ,..., [Tm]k(m) }
следует из леммы 4.21. 
Лемма 4.22 дает подход к восстановлению однозначных НКС-грамматик по
известному образцу Ω и параметру kinf.
Метод 4.23 (Восстановление однозначных КС-языков)
Шаг 1. Построить множество сетей
КЛ(Ω,kinf) = {T' - k-Л-сеть | k ≥ kinf, L(T') ⊂ Ω}.
Шаг 2. Для каждого подмножества T ⊂ КЛ(Ω,kinf) такого, что
⊕ T есть П-сеть, последовательно выполнить действия:
(а) (Структурирование) построить сеть T = ⊕( T ∪ {T #});
(б) (Обобщение) используя определение 4.13, построить множество
грамматик G(T);
(в) используя определение 4.20, построить подмножество решающих
грамматик {доо(G,Ω) | G ∈ G(T)}. 
Теорема.
Задача грамматического вывода разрешима для однозначного
КС-языка источника Lи, полной положительной последовательности
образцов {Ωi | i ≥ 1} и метода восстановления 4.23.
Доказательство. Зафиксируем произвольный однозначный
КС-язык источника Lи и некоторую соответствующую ему
НКС-грамматику G = < N, Σ, P, S >. Кроме того, зафиксируем некоторое
значение параметра kinf.
Рассмотрим сеть TS,n для n = ||N|| + E(G).
Из леммы 4.22 следует, что для сети TS,n существует
восстанавливающий набор k-Л-подсетей [T1]k(1), ..., [Tm]k(m).
Положим I = max { J0, J1, ..., Jm}, где
J0 = max {|x| | x ∈ ост(G) },
Jj = max {|x| | x ∈ L([Tj]k(j)) } (j=1, ..., m).
Так как последовательность образцов является полной положительной, то среди
ее членов найдется образец Ωi(I) такой, что
{ x ∈ L | |x| ≤ I} ⊂ Ωi(I).
При этом, L([Tj]k(j)) ⊂ Ωi(I)
для любого j = 1, ..., m.
Из определения множества КЛ (см. шаг 1 метода 4.23)
следует, что КЛ(Ωi(I),kinf) содержит сеть T'
изоморфную [Tj]k(j) ( j=1, ..., m ).
Поскольку операция ⊕ использует исключительно разметку
ребер, то на шаге 2.а (в частности) будет построена сеть
T = ⊕{T#, T'1, ..., T'm} ≈n TS,n.
Из теоремы 4.14 следует, что среди грамматик G(T),
построенных на шаге 2.б, найдется грамматика, эквивалентная
Gост.
Выбор числа I гарантирует, что ост(G) ⊂ Ωi(I).
Следовательно, грамматика доо(осн(G),Ωi(I)) эквивалентна G.

Метод 4.23 является параметрическим, причем формальная применимость метода
не зависит от значения параметра kinf. По своему смыслу
kinf задает минимальное количество конкретных проявлений,
достаточное для принятия решения о существовании той или иной закономерности.
С практической точки зрения, варьируя параметром kinf, можно
сократить количество k-Л-сетей, построенных на первом шаге, что позволит
сократить перебор на шаге 2. В любом случае значение kinf зависит
от контекста применения метода восстановления.
4.4.3 Эвристический метод восстановления контекстно-свободных языков
В реальных задачах чаще всего задается не последовательность, а один
образец, в котором, к тому же, могут отсутствовать отдельные предложения.
В этих случаях предлагается использовать эвристический метод восстановления,
постулирующий некоторые частные свойства грамматик, но позволяющий пополнять
образец. Рассмотрим эти свойства.
Для НКС-грамматики G = < N, Σ, P, S > определим два класса
цепочек:
RR(G,A) = { α | A =>+G α } и
L(G,α) = { x ∈ Σ* | α =>*G x }.
Приведем три свойства однозначных НКС-грамматик.
Свойство 1. Множество { L(G,α) | α ∈ R(G,S) }
образует наименьшее разбиение языка L(G) подмножествами L(G,β),
где β ∈ RR(G,S). 
Свойство 2. Пусть α = z0A1z1...Anzn
- цепочка из RR(G,S) и n > 1.
Тогда строковое уравнение (относительно A1, ..., An)
z0A1z1...Anzn = x, x ∈ L(G,α),
имеет решение Ai = yi,
причем yi ∈ L(G,Ai) (i=1,...,n).
(Такие решения (y1, ..., yn) будем называть правильными.)

Первое свойство задает процедуру выявления множества R(G,S)
из более широкого множества цепочек RR(G,S). Второе свойство
позволяет перейти от восстановления множества R(G,S) (по
известному образцу Ω) к восстановлению множеств R(G,Ai)
(по множеству решений типа yi).
Свойство 3. Пусть α = z0A1...Anzn
- цепочка из RR(G,S) и n > 1. Тогда существуют, по-крайней мере,
две цепочки x1 и x2
из L(G,α) такие, что правильные решения (y11, ..., y1n) и
(y21, ..., y2n) соответствующих строковых уравнений
z0A1z1...Anzn = x1 и z0A1z1...Anzn = x2
удовлетворяют условиям y1i ≠ y2i (i=1,...,n).

Свойство 3 дает подход к формированию некоторого
подмножества цепочек из RR(G,S).
Рассмотрим две подзадачи, которые решаются в ходе
восстановления грамматик эвристическим методом.
Задача 4.24 (Задача восстановления общей структуры двух цепочек).
Дано. Две цепочки символов x1 и x2.
Требуется. Построить множество SV(x1,x2) цепочек
вида z0A1z1...Anzn,
удовлетворяющих условиям:
| (1) |
уравнения z0A1z1...Amzm = x1
и z0A1z1...Amzm = x2
имеют по-крайней мере по одному решению
(y11, ..., y1n)
и (y21, ..., y2n), причем yij ≠ e (i=1,2; j=1,...,n);
|
| (2) |
если цепочки α = z'0A1z'1...Amz'm
и β = z0A1z1...Amm
удовлетворяют условию (1) и |z'0z'1...z'm|
< |z0z1...zm|,
то α ∉ SV(x1,x2).
|

Условию (1) всегда удовлетворяют тривиальные, но бесполезные цепочки,
состоящие из единственного нетерминала A1. Условие (2) позволяет
найти "самое нетривиальное" решение и, в частности, гарантирует равенство
SV(x,x) = { x }, которое должно выполняться по смыслу задачи. В общем случае
задача 4.24 не имеет единственного решения, например,
SV(ab,aab) = {A1b, aA1}.
Метод решения задачи 4.24 для цепочек
x1 = a1...an и
x2 = b1...bm
существенно использует ориентированный граф специального вида.
Вершинами графа являются элементы множества
{(i,j) | ai = bj},
а множество ребер образуют все пары вершин
((i,j),(i',j')), для которых либо i' = i+1 и j' = j+1, либо
i' > i+1 и j' > j+1. В том же случае, когда граф построить не
удается, в качестве решения принимается множество цепочек
{ A1...Ai | i = 2, ..., min(m,n) }.
В соответствии с процедурой выявления множества R(G,S), для каждой цепочки
β ∈ RR(G,S) необходимо построить множество L(G,β) или его
конечное подмножество Ω(β).
Задача построения множества Ω(β) по образцу Ω и цепочке
β обладает двумя особенностями. Во-первых, эта задача может иметь
несколько решений. Во-вторых, при решении именно этой задачи появляется
возможность пополнить заданный образец новыми предложениями. При этом
необходимо задать априорную оценку полноты образца - параметр ρ.
Будем полагать, что множество Ω(β) задается в виде
L(G(Ω,β)) ∩ Ω, где G(Ω,b) - нерекурсивная
грамматика, удовлетворяющая некоторым требованиям.
Условие 4.25
| (1) |
Грамматика G(Ω,β) для
β = z0A1z1...Anzn
имеет вид:
S → β
Ai → Ωi (i=1, ..., n),
где Ωi ∈ Σ+
и ||Ωi|| > 1
|
| (2) |
Для любой цепочки yi ∈ Ωi существуют цепочки yj ∈ Ωj
(j =1, ..., i-1,i+1, ..., n) такие, что z0y1z1...ynzn ∈ Ω
|
| (3) |
Грамматика G(Ω,β) является однозначной
|
| (4) |
| ||Ω(β)|| | |
| ≥ ρ
где ρ - параметр метода
|
| ||L(G(Ω,β))|| | |
|
| (5) |
Множества Ωi (i=1, ... ,n) нельзя пополнить
новыми цепочками с сохранением условий (1)-(4).
|

Задача 4.26
Дано. Образец Ω, цепочка β и параметр ρ ∈ (0,1].
Требуется. Построить GSV(Ω,β) - множество всех грамматик
G(Ω,β), удовлетворяющих условию 4.25. 
Задача 4.26 решается перебором подмножеств
Ωi,all ⊂ Ωi
(i=1,...,n), где множество Ωi,all есть
{ yi | (... yi, ...)
- решение уравнения β = x для нек. x из Ω }
Отметим, что результатом решения задачи 4.26
может быть пустое множество грамматик.
Определим две операции над нерекурсивными грамматиками
G1 = < N1, Σ1, P1, S1 >
и
G2 = < N2, Σ2, P2, S2 >.
Прежде всего переименуем
нетерминалы таким образом, что N1 ∩ N2 = ∅.
(1) Операция подстановки (вместо нетерминала A ∈ N1)
строит
новую грамматику п(G1,A,G2) с правилами вывода
(P1 ∪ (A → R(G2,S2)) ∪ P2)
\ (A → R(G1,A))
\ (S2 → R(G2,S2)).
(2) Операция слияния строит новую грамматику
p(G1,G2) с правилами вывода
(P1 ∪ (S1 → R(G2,S2)) ∪ P2)
\ (S2 → R(G2,S2));
Будем полагать, что при m > 2
p(G1, ..., Gm) = p(p(G1,...,Gm-1),Gm).

Пусть Ω - некоторое множество предложений и ρ - число из (0,1].
Определим множество грамматик GSV(Ω) как результат следующей
последовательности вычислений:
| (1) |
| RR = ( |
∪ |
SV(x,y)) \ {A1}; |
| x ∈ Ω | |
| y ∈ Ω | |
|
| (2) |
|
| (3) |
GGнр = { {G1, ..., Gm } ⊂ GG | (*) };
(В данном случае условие (*) означает, что множества
L(G1) ∩ Ω, ..., L(Gm) ∩ Ω
образуют наименьшее
разбиение образца Ω подмножествами L(G) ∩ Ω, G ∈ GG.)
|
| (4) |
GSV(Ω) = { p(G1,...,Gm) | { G1, ..., Gm } ∈ GGнр }.
|
При этом будем говорить, что образец Ω является нетривиальным,
если m < ||Ω||. 
Приведем метод структурирования образца Ω. Результатом
вычисления является множество нерекурсивных грамматик
G = G(Ω,ρ),
где ρ - параметр метода.
Метод 4.27 (Эвристический метод структурирования)
Шаг 1. Положить G = { < {S}, Σ, S → Ω, S > }.
Шаг 2. Если среди грамматик множества G найдется
грамматика G такая, что для некоторого нетерминала A R(G,A) ⊂ Σ*
и R(G,A) - нетривиальный образец, то
(a) преобразовать множество G
G = (G \ {G}) ∪ { п(G,A,G') | G' ∈ GSV(R(G,A)) };
(б) повторить шаг 2.  Каждую нерекурсивную грамматику из множества
G(Ω,ρ) можно очевидным образом преобразовать
в конечную П-сеть. При этом появляется возможность применить к ней метод
обобщения 4.13 и построить множество решающих КС-грамматик общего вида.
С точки зрения разрешимости задачи грамматического вывода (методом 4.27),
рассчитывать на восстановление КС-грамматики Gи = < N, Σ, P, S >
можно лишь в том случае, когда образец содержит достаточное количество
предложений глубиной вывода не более
||N|| + E(Gи).
Главный недостаток эвристического метода состоит в том, что множество
G(Ω,ρ) может содержать слишком много
различных грамматик. Причиной тому является независимость друг от друга
множеств GSV(R(G,A)). Вместе с тем, совокупность этих множеств можно
рассматривать как некоторую систему альтернатив (см. определение 2.1),
в которой двум грамматикам сопоставляется один и тот же факт, если их внешние
структуры совпадают. (Речь идет об отношении типа ≈.) При таком подходе,
на этапе структурирования генерируются лишь те грамматики, которым
соответствуют наборы фактов из класса распознавания системы альтернатив.
В конечном итоге, описанная модификация эвристического метода позволяет
отсечь "неинтересные" грамматики, по-разному структурирующие одинаковые
или сходные образцы.
Методы восстановления формальных грамматик используется:
— для синтеза схем управления (п. 5.4);
— в методе доводки имен атрибутов (п. 5.5).
|